Question

【题目】已知函数f（x）=2 sinxcosx+2cos2x﹣1（x∈R） （Ⅰ）求函数f（x）的最小正周期及在区间[0， ]上的最大值和最小值；
（Ⅱ）若f（x0）= ，x0∈[ ， ]，求cos2x0的值．

Answer 1

【答案】解：（1）由f（x）=2 sinxcosx+2cos2x﹣1，得 f（x）= （2sinxcosx）+（2cos2x﹣1）= sin2x+cos2x=2sin（2x+ ）
所以函数f（x）的最小正周期为π．
因为f（x）=2sin（2x+ ）在区间[0， ]上为增函数，在区间[ ， ]上为减函数，
又f（0）=1，f（ ）=2，f（ ）=﹣1，所以函数f（x）在区间[0， ]上的最大值为2，最小值为﹣1．
（Ⅱ）由（1）可知f（x0）=2sin（2x0+ ）
又因为f（x0）= ，所以sin（2x0+ ）=
由x0∈[ ， ]，得2x0+ ∈[ ， ]
从而cos（2x0+ ）=﹣ =﹣ ．
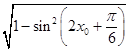所以
cos2x0=cos[（2x0+ ）﹣ ]=cos（2x0+ ）cos +sin（2x0+ ）sin =
【解析】先将原函数化简为y=Asin（ωx+φ）+b的形式（1）根据周期等于2π除以ω可得答案，又根据函数图像和性质可得在区间[0， ]上的最值．（2）将x0代入化简后的函数解析式可得到sin（2x0+ ）= ，再根据x0的范围可求出cos（2x0+ ）的值， 最后由cos2x0=cos（2x0+ ）可得答案．