
分析 (1)利用定圆⊙F1:x2+y2+4x+3=0,⊙F2:x2+y2-4x-5=0,动圆M与圆F1、F2都外切或都内切,结合双曲线的定义,即可得出轨迹方程.
(2)求出直线方程,即可求|AB|.
解答 解:(1)⊙F1:x2+y2+4x+3=0和,⊙F2:x2+y2-4x-5=0,
即圆F1:(x+2)2+y2=1和F2:(x-2)2+y2=9.
设动圆的圆心P(x,y),半径为R,
由题意,与两已知圆都外切或都内切,有|PC1|=R+3,|PC2|=R+1,|PC1|-|PC2|=2<4,
∴点P的轨迹是双曲线的一支,方程为${x^2}-\frac{y^2}{3}=1({x<-1})$;
(2)令直线l:x=my-2,从而${d_{{F_2}→1}}=\frac{4}{{\sqrt{1+{m^2}}}}$,
∴9=$\frac{16}{1+{m}^{2}}$+1,
根据对称性,不妨设m=1,
由$\left\{\begin{array}{l}{{x}^{2}-\frac{{y}^{2}}{3}=1}\\{y=x+2}\end{array}\right.$,可得2x2-4x-7=0,
∴|AB|=$\sqrt{2}•\sqrt{4+4•\frac{7}{2}}$=6.
点评 本题考查轨迹方程,考查直线与双曲线的位置关系,考查学生分析解决问题的能力,属于中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:解答题
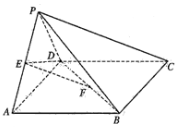 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,E,F分别为PA,BD的中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,E,F分别为PA,BD的中点,PA=PD=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 432 | B. | 384 | C. | 308 | D. | 288 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α=$\frac{π}{4}$,β=-$\frac{π}{4}$ | B. | $α=\frac{2π}{3},β=\frac{π}{6}$ | C. | $α=\frac{π}{3},β=\frac{π}{6}$ | D. | $α=\frac{5π}{6},β=\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果m⊥n,m⊥α,n∥β,那么α⊥β | |
| B. | 如果m⊥α,n∥α,那么m⊥n | |
| C. | α∥β,m?α,那么m∥β | |
| D. | 如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com