
数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为 .
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷(解析版) 题型:解答题
东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本g(n)与科技成本的投入次数n的关系是g(n)=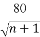 .若水晶产品的销售价格不变,第n次投入后的年利润为f(n)万元.
.若水晶产品的销售价格不变,第n次投入后的年利润为f(n)万元.
(1)求出f(n)的表达式.
(2)求从今年算起第几年利润最高?最高利润为多少万元?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:选择题
已知a1,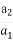 ,
,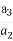 ,…,
,…, ,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
(A)25050(B)24950(C)2100(D)299
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
三段论:“①所有的中国人都坚强不屈;②玉树人是中国人;③玉树人一定坚强不屈”中,其中“大前提”和“小前提”分别是( )
(A)①② (B)①③
(C)②③ (D)②①
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:解答题
已知各项都不相等的等差数列{an}的前6项和为60,且a6为a1和a21的等比中项.
(1)求数列{an}的通项公式.
(2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=3,求数列{ }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则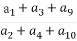 =( )
=( )
(A)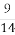 (B)
(B)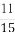 (C)
(C)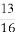 (D)
(D)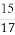
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:填空题
已知点P(2,t)在不等式组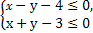 表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:解答题
设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围.
(2)求{an}前n项和Sn最大时n的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十六选修4-2第三节练习卷(解析版) 题型:解答题
若矩阵A有特征值λ1=2,λ2=-1,它们所对应的特征向量分别为e1=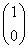 和e2=
和e2=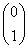 .
.
(1)求矩阵A.
(2)求曲线x2+y2=1在矩阵A的变换下得到的新曲线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com