
【题目】在平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,直线l:
,直线l:![]() 交椭圆C于A,B两点,且
交椭圆C于A,B两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆C的方程;
(2)若线段![]() 的中点为P,直线
的中点为P,直线![]() 与椭圆C交于M,N两点,且
与椭圆C交于M,N两点,且![]() ,求直线l的方程.
,求直线l的方程.
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数).证明:对任意
的导函数).证明:对任意![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由正方形![]() ,直角梯形
,直角梯形![]() ,三角形
,三角形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
,![]() ,将其沿
,将其沿![]() ,
,![]() 折起使得
折起使得![]() 与
与![]() 重合,连接
重合,连接![]() ,如图2.
,如图2.
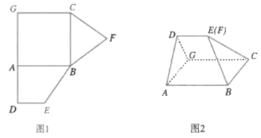
(1)证明:图2中的![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
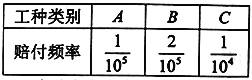
已知![]() 三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)求保险公司在该业务所或利润的期望值;
(2)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工,企业开展这项工作的固定支出为每年12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面ABCD,底面ABCD是等腰梯形,
平面ABCD,底面ABCD是等腰梯形,![]() ,
,![]() .
.
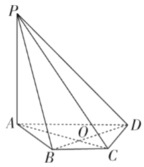
(1)证明:![]() 平面PAC;
平面PAC;
(2)若![]() ,
,![]() ,设
,设![]() ,且
,且![]() ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 分别为菱形
分别为菱形![]() 的边
的边![]() 的中点,将菱形沿对角线
的中点,将菱形沿对角线![]() 折起,使点
折起,使点![]() 不在平面
不在平面![]() 内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
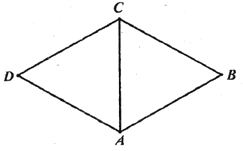
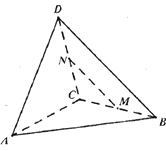
①![]() 平面
平面![]() ;②异面直线
;②异面直线![]() 与
与![]() 所成的角为定值;③在二面角
所成的角为定值;③在二面角![]() 逐渐渐变小的过程中,三棱锥
逐渐渐变小的过程中,三棱锥![]() 的外接球半径先变小后变大;④若存在某个位程,使得直线
的外接球半径先变小后变大;④若存在某个位程,使得直线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面,平面
所在平面,平面![]() 平面
平面![]() ,且
,且![]() ,且
,且![]() .
.

(1)设点![]() 为棱
为棱![]() 中点,在面
中点,在面![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请证明,若不存在,说明理由;
?若存在,请证明,若不存在,说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com