
【题目】某保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
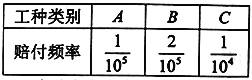
已知![]() 三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)求保险公司在该业务所或利润的期望值;
(2)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工,企业开展这项工作的固定支出为每年12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
【答案】(Ⅰ)详见解析;(Ⅱ) 方案2.
【解析】试题分析:(Ⅰ)设工种![]() 职工的每份保单保险公司的收益为随机变量
职工的每份保单保险公司的收益为随机变量![]() ,可得其分布列,分别求解数学期望,即可得到该工资的期望值;
,可得其分布列,分别求解数学期望,即可得到该工资的期望值;
(Ⅱ)分别求出方案1和方案2中企业每年安全支出与固定开支,即可作出比较得到结论.
试题解析:
(Ⅰ)设工种A、B、C职工的每份保单保险公司的收益为随机变量X、Y、Z,则X、Y、Z的分布列为
X | 25 |
| |
P |
|
| |
Y | 25 |
| |
P |
|
| |
Z | 40 |
| |
P |
|
| |
保险公司的期望收益为
![]() ;
;
![]() ;
;
![]() ;
;
保险公司的利润的期望值为![]() ,
,
保险公司在该业务所获利润的期望值为9万元.
(Ⅱ)方案1:企业不与保险公司合作,则企业每年安全支出与固定开支共为:
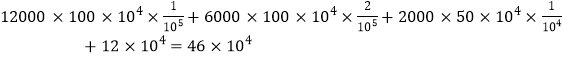 ,
,
方案2:企业与保险公司合作,则企业支出保险金额为:
![]() ,
,
![]() ,故建议企业选择方案2.
,故建议企业选择方案2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本![]() (万元)可以看成月产量
(万元)可以看成月产量![]() (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本![]() (万元)关于月产量
(万元)关于月产量![]() (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程为
的方程为![]() ,其焦点为
,其焦点为![]() ,
,![]() 为过焦点
为过焦点![]() 的抛物线
的抛物线![]() 的弦,过
的弦,过![]() 分别作抛物线的切线
分别作抛物线的切线![]() ,设
,设![]() 相交于点
相交于点![]() .
.
(1)求![]() 的值;
的值;
(2)如果圆![]() 的方程为
的方程为![]() ,且点
,且点![]() 在圆
在圆![]() 内部,设直线
内部,设直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗器械公司在全国共有![]() 个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这
个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这![]() 个销售点的年销量绘制出如下的频率分布直方图.
个销售点的年销量绘制出如下的频率分布直方图.
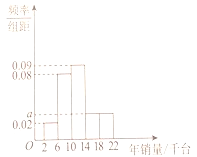
(1)完成年销售任务的销售点有多少个?
(2)若用分层抽样的方法从这![]() 个销售点中抽取容量为
个销售点中抽取容量为![]() 的样本,求该五组
的样本,求该五组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:千台)中每组分别应抽取的销售点数量.
,(单位:千台)中每组分别应抽取的销售点数量.
(3)在(2)的条件下,从该样本中完成年销售任务的销售点中随机选取![]() 个,求这两个销售点不在同一组的概率.
个,求这两个销售点不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的左焦点
的左焦点![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,若
,若![]() 为等腰直角三角形,求
为等腰直角三角形,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() ,
,![]() 两点间的距离
两点间的距离![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查中国及美国的高中生在“家”、“朋友聚集的地方”、“个人空间”这三个场所中感到最幸福的场所是哪个,从中国某城市的高中生中随机抽取了55人,从美国某城市高中生中随机抽取了45人进行答题。中国高中生的答题情况:选择“家”的高中生的人数占![]() ,选择“朋友聚集的地方”的高中生的人数占
,选择“朋友聚集的地方”的高中生的人数占![]() ,选择“个人空间”的高中生的人数占
,选择“个人空间”的高中生的人数占![]() ,美国高中生的答题情况:选择“家”的高中生的人数占
,美国高中生的答题情况:选择“家”的高中生的人数占![]() ,选择“朋友聚集的地方”的高中生的人数占
,选择“朋友聚集的地方”的高中生的人数占![]() ,选择“个人空间”的高中生的人数占
,选择“个人空间”的高中生的人数占![]() 。
。
(1)请根据以上调查结果将下面的2X2列联表补充完整,并判断能否有95%的把握认为恋家(在家里感到最幸福)与国别有关;
在家里感到最幸福 | 在其他场所感到最幸福 | 总计 | |
中国高中生 | |||
美国高中生 | |||
总计 |
(2)从被调查的不“恋家”的美国高中生中,用分层抽样的方法随机选出4人接受进一步调查,再从4人中随机选出2人到中国交流学习,求2人中含有在“个人空间”感到最幸福的高中生的概率。
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.8 |
附:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com