
三个半径为R的球互相外切,且每个球都同时与另两个半径为r的球外切.如果这两个半径为r的球也互相外切,则R与r的关系是( )
A.R=r B.R=2r C.R=3r D.R=6r
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:2014-2015学年贵州省高三模拟考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)【选修4—5:不等式选讲】
已知函数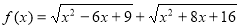 .
.
(1)求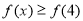 的解集;
的解集;
(2)设函数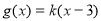 ,
,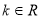 ,若
,若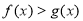 对任意的
对任意的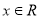 都成立,求实数
都成立,求实数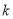 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:填空题
已知各项均为正数的等比数列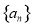 的首项
的首项 ,公比为
,公比为 ,前
,前 项和为
项和为 ,若
,若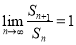 ,则公比为
,则公比为 的取值范围是_____________.
的取值范围是_____________.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:解答题
设A、B、C是半径为1的球面上的三点,B、C两点间的球面距离为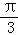 ,点A与B、C两点间的球面距离均为
,点A与B、C两点间的球面距离均为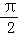 ,O为球心,
,O为球心,
求:(1)∠AOB、∠BOC的大小;
(2)球心O到截面ABC的距离.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,若OM=ON=3,则两圆圆心的距离MN= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2010•内江二模)如图,是一个由三根细铁杆PA、PB、PC组成的支架,三根杆的两两夹角都是60°,一个半径为1的球放在支架内,使杆与球相切,则球心到点P的距离是( )
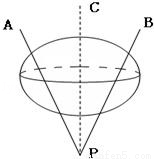
A.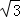 B.
B. C.2 D.
C.2 D.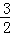
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
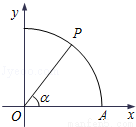
(Ⅰ)若点P的坐标是(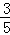 ,
, ),求cos2
),求cos2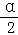 ﹣sin2
﹣sin2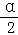 +2sin
+2sin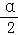 cos
cos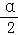 的值;
的值;
(Ⅱ)求函数f(α)=sinα+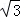 cosα的值域.
cosα的值域.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
设f(x)=sinxcosx,那么f′(x)=( )
A.﹣cosxsinx B.cos2x C.sinx+cosx D.cosx﹣sinx
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
若平面α的法向量为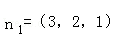 ,平面β的法向量为
,平面β的法向量为 ,则平面α与β夹角(锐角)的余弦是( )
,则平面α与β夹角(锐角)的余弦是( )
A.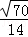 B.
B.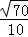 C.
C.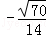 D.﹣
D.﹣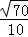
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com