
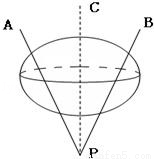
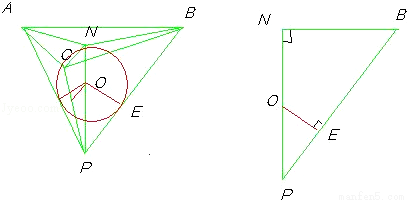
(2010•内江二模)如图,是一个由三根细铁杆PA、PB、PC组成的支架,三根杆的两两夹角都是60°,一个半径为1的球放在支架内,使杆与球相切,则球心到点P的距离是( )
A.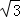 B.
B. C.2 D.
C.2 D.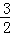
A
【解析】
试题分析:根据小球与三根杆分别切于E、F、G点,在三根杆上取相等的长度,令PA=PB=PC,根据三根杆的两两夹角都是60度,可推断出△PAC、PBC、PAB均为等边三角形,且全等.可知四面体P﹣ABC中每条棱均相等.延长PO至与三角形交于N点,判断出NB:PB=1: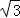 单独取三角形PNB分析,进而根据OP:OE=PB:NB求得半径OE,进而求得OP,即球心道点P的距离.
单独取三角形PNB分析,进而根据OP:OE=PB:NB求得半径OE,进而求得OP,即球心道点P的距离.
【解析】
如图:将小球放进支架中,小球与三根杆分别切于E、F、G点,在三根杆上取相等的长度,令PA=PB=PC,
∵三根杆的两两夹角都是60度,
∴△PAC、PBC、PAB均为等边三角形,且全等.可知四面体P﹣ABC中每条棱均相等.
延长PO至与三角形交于N点.
NB:PB=1: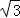
单独取三角形PNB分析,易得△OEP与∽△PNB.
∴OP:OE=PB:NB=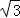 :1,OE为半径1,推出OP为
:1,OE为半径1,推出OP为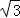 .
.
即球心到点P的距离是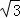
故选A


科目:高中数学 来源:2014-2015学年贵州省高三模拟考试文科数学试卷(解析版) 题型:解答题
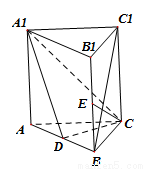
(本小题满分12分)如图,直三棱柱 中,
中,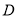 ,
,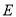 分别是
分别是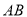 ,
, 的中点.
的中点.
(1)证明: 平面
平面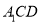 ;
;
(2)设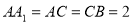 ,
, ,求四棱锥
,求四棱锥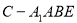 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:填空题
如图,一个底面半径为R的圆柱被与其底面所成角为θ(0°<θ<90°)的平面所截,截面是一个椭圆,
当θ为30°时,这个椭圆的离心率为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
已知棱长等于2的正四面体的四个顶点在同一个球面上,则球的半径长为 ,球的表面积为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
三个半径为R的球互相外切,且每个球都同时与另两个半径为r的球外切.如果这两个半径为r的球也互相外切,则R与r的关系是( )
A.R=r B.R=2r C.R=3r D.R=6r
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某校高二年级某班的数学课外活动小组有6名男生,4名女生,从中选出4人参加数学竞赛考试,用X表示其中男生的人数,
(1)请列出X的分布列;
(2)根据你所列的分布列求选出的4人中至少有3名男生的概率.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n.
(1)算国徽面朝上不同次数的概率并填入下表: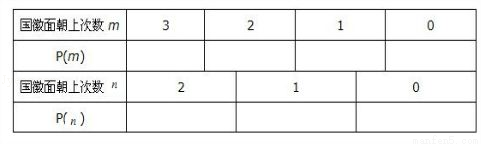
(2)现规定:若m>n,则甲胜;若n≥m,则乙胜.你认为这种规定合理吗?为什么?
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
函数f(x)=sin2x的导数f′(x)=( )
A.2sinx B.2sin2x C.2cosx D.sin2x
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
在三棱柱ABC﹣A1B1C1中,底面为棱长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值是( )
A.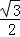 B.
B.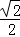 C.
C.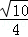 D.
D.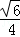
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com