练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f（x）=sin2x的导数f′（x）=（ ）

    A.2sinx B.2sin2x C.2cosx D.sin2x

    D

    【解析】

    试题分析：将f（x）=sin2x看成外函数和内函数，分别求导即可．

    【解析】

    将y=sin2x写成，

    y=u2，u=sinx的形式．

    对外函数求导为y′=2u，

    对内函数求导为u′=cosx，

    故可以得到y=sin2x的导数为

    y′=2ucosx=2sinxcosx=sin2x

    故选D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014-2015学年上海市高二上学期第一次月考数学试卷（解析版） 题型：填空题

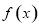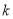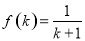    已知是定义域为正整数集的函数，具有如下性质：对于定义域内任意的，如果成立，则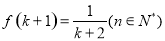成立，那么下列命题正确的是___

    ①若成立，则对于任意，均有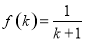

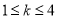    ②若成立，则对于任意，均有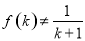

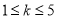    ③若成立，则对于任意，均有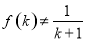

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系（解析版） 题型：选择题

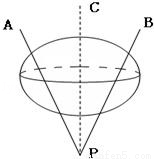
    （2010•内江二模）如图，是一个由三根细铁杆PA、PB、PC组成的支架，三根杆的两两夹角都是60°，一个半径为1的球放在支架内，使杆与球相切，则球心到点P的距离是（ ）

    A.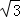 B. C.2 D.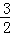

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-3 2.2超几何分布练习卷（解析版） 题型：填空题

    有一批产品，其中有6件正品和4件次品，从中任取3件，至少有2件次品的概率为 ．

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷（解析版） 题型：?????

    设f（x）=sinxcosx，那么f′（x）=（ ）

    A.﹣cosxsinx B.cos2x C.sinx+cosx D.cosx﹣sinx

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷（解析版） 题型：?????

    设f（x）=cos22x，则=（ ）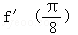

    A.2 B. C.﹣1 D.﹣2

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷（解析版） 题型：?????

    （2012•桂林模拟）设a∈R，函数f（x）=ex+a•e﹣x的导函数是f′（x），且f′（x）是奇函数．若曲线y=f（x）的一条切线的斜率是，则切点的横坐标为（ ）

    A.ln2 B.﹣ln2 C.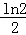 D.

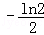
    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷（解析版） 题型：?????

    （2012•九江一模）已知f（x）是定义在（0，+∞）上的单调函数，且对任意的x∈（0，+∞），都有f[f（x）﹣x3]=2，则方程f（x）﹣f′（x）=2的解所在的区间是（ ）

    A.（0，1） B.（1，2） C.（2，3） D.（3，4）

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷（解析版） 题型：填空题

    已知函数f（x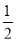）＝（x2＋a）的图象在点Pn（n，f（n））（n∈N*）处的切线ln的斜率为kn，直线ln交x轴，y轴分别于点An（xn，0），Bn（0，yn），且y1＝－1．给出以下结论：

    ①a＝－1；

    ②记函数g（n）＝xn（n∈N*），则函数g（n）的单调性是先减后增，且最小值为；

    ③当n∈N*时，；

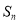    ④当n∈N*时，记数列的前项和为，则．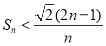

    其中，正确的结论有 （写出所有正确结论的序号）

    查看答案和解析>>

    同步练习册答案