
甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n.
(1)算国徽面朝上不同次数的概率并填入下表: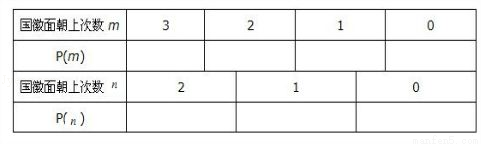
(2)现规定:若m>n,则甲胜;若n≥m,则乙胜.你认为这种规定合理吗?为什么?
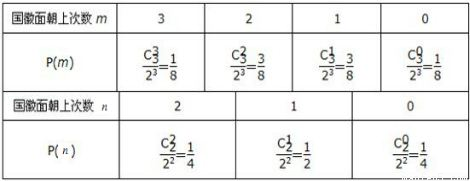
(1)
(2)甲和乙获胜的概率老都是,即获胜机会相等,所以这种规定是合理的.
【解析】
试题分析:首先分析题目对于(1)可直接根据相互独立事件概率乘法公式求得每个事件的概率填入表格即可.
对于(2)可根据(1)求得的数据,分别求出若m>n甲胜的概率和n≥m乙胜的概率.判断它们的概率是否都相等且等于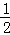 ,即判断甲乙获胜的概率是否相等,即可判断规定是否合理.
,即判断甲乙获胜的概率是否相等,即可判断规定是否合理.
【解析】
(1)根据相互独立事件概率乘法公式得:

(2)这种规定是合理的.这是因为甲获胜,则m>n
当m=3时,n=2,1,0,其概率为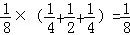
当m=2时,n=1,0,其概率为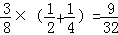 ;
;
当m=1时,n=0,其概率为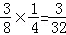 ;
;
∴甲获胜的概率为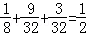
若乙获胜,则m≤n
当n=2时,m=2,1,0,其概率为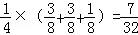 ;
;
当n=1时,m=1,0,其概率为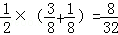 ;
;
当n=0时,m=0,其概率为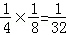 ;
;
∴乙获胜的概率为
甲和乙获胜的概率老都是,即获胜机会相等,所以这种规定是合理的.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:解答题
设A、B、C是半径为1的球面上的三点,B、C两点间的球面距离为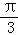 ,点A与B、C两点间的球面距离均为
,点A与B、C两点间的球面距离均为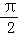 ,O为球心,
,O为球心,
求:(1)∠AOB、∠BOC的大小;
(2)球心O到截面ABC的距离.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
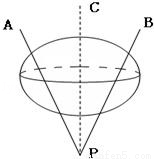
(2010•内江二模)如图,是一个由三根细铁杆PA、PB、PC组成的支架,三根杆的两两夹角都是60°,一个半径为1的球放在支架内,使杆与球相切,则球心到点P的距离是( )
A.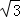 B.
B. C.2 D.
C.2 D.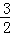
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
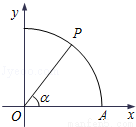
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
(Ⅰ)若点P的坐标是(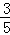 ,
, ),求cos2
),求cos2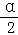 ﹣sin2
﹣sin2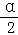 +2sin
+2sin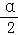 cos
cos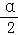 的值;
的值;
(Ⅱ)求函数f(α)=sinα+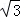 cosα的值域.
cosα的值域.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:填空题
有一批产品,其中有6件正品和4件次品,从中任取3件,至少有2件次品的概率为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
设f(x)=sinxcosx,那么f′(x)=( )
A.﹣cosxsinx B.cos2x C.sinx+cosx D.cosx﹣sinx
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
(2012•桂林模拟)设a∈R,函数f(x)=ex+a•e﹣x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.ln2 B.﹣ln2 C.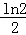 D.
D.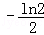
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
(2014•合肥二模)已知正方体ABCD﹣A1B1C1D1中,线段B1A1,B1C1上(不包括端点)各有一点P,Q,且B1P=B1Q,下列说法中,不正确的是( )
A.A,C,P,Q四点共面
B.直线PQ与平面BCC1B1所成的角为定值
C.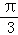 <∠PAC<
<∠PAC<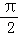
D.设二面角P﹣AC﹣B的大小为θ,则tanθ的最小值为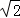
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com