
(2014•合肥二模)已知正方体ABCD﹣A1B1C1D1中,线段B1A1,B1C1上(不包括端点)各有一点P,Q,且B1P=B1Q,下列说法中,不正确的是( )
A.A,C,P,Q四点共面
B.直线PQ与平面BCC1B1所成的角为定值
C.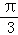 <∠PAC<
<∠PAC<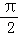
D.设二面角P﹣AC﹣B的大小为θ,则tanθ的最小值为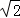
D
【解析】
试题分析:利用平面的基本性质判断A的正误;直线与平面所成角判断B是正误;通过特例判断C的正误;通过二面角的大小求解判断D的正误.
【解析】
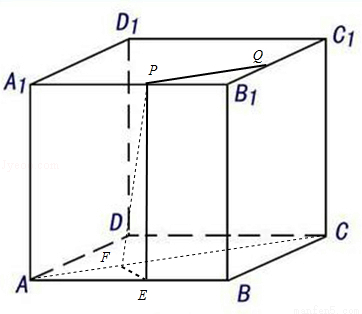
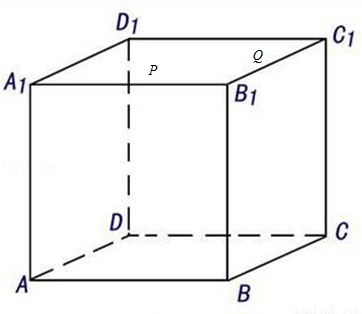
正方体ABCD﹣A1B1C1D1中,线段B1A1,B1C1上(不包括端点)各有一点P,Q,且B1P=B1Q,如图:
当PQ连线与AC平行时,A,C,P,Q四点共面,
∴A不正确;
直线PQ与平面BCC1B1所成的角为定值,显然不正确,P在平面BCC1B1的射影是B1,Q如果是定点,直线PQ与平面BCC1B1所成的角为变值,∴B不正确;
对于C,当P在A1B1 的中点时,不妨设作法的棱长为2,cos∠PAC= <0,∠PAC是钝角,∴
<0,∠PAC是钝角,∴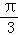 <∠PAC<
<∠PAC<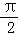 不正确;
不正确;
对于D,作PE⊥AB于E,过E作EF⊥AC于F,θ=∠PFE,则tanθ的最小值时EF最大,此时P在B1,tanθ=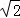 ,
,
∴D正确.
故选:D.


科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n.
(1)算国徽面朝上不同次数的概率并填入下表: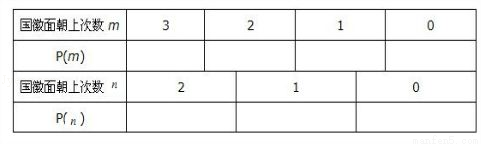
(2)现规定:若m>n,则甲胜;若n≥m,则乙胜.你认为这种规定合理吗?为什么?
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
函数f(x)= ex(sinx+cosx)在区间[0,
ex(sinx+cosx)在区间[0, ]上的值域为( )
]上的值域为( )
A.[ ,
, e
e ] B.(
] B.( ,
, e
e ) C.[1,e
) C.[1,e ] D.(1,e
] D.(1,e )
)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
在三棱柱ABC﹣A1B1C1中,底面为棱长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值是( )
A.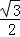 B.
B.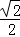 C.
C.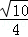 D.
D.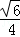
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
在正方体ABCD﹣A1B1C1D1中,点M为棱AA1的中点,则直线BC1与平面MC1D1所成角的正弦值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷(解析版) 题型:选择题
空间中,与向量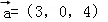 同向共线的单位向量
同向共线的单位向量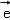 为( )
为( )
A.
B. 或
或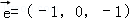
C.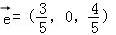
D.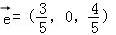 或
或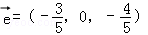
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知椭圆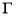 :
: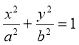 (
( )的右焦点为
)的右焦点为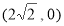 ,且过点
,且过点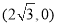 .
.
(Ⅰ)求椭圆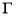 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、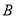 ,且
,且 .若点
.若点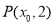 满足
满足 ,求
,求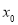 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:选择题
命题“若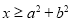 ,则
,则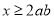 ”的逆命题是
”的逆命题是
(A)若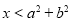 ,则
,则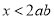
(B)若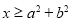 ,则
,则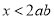
(C)若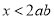 ,则
,则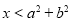
(D)若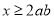 ,则
,则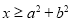
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com