
函数f(x)= ex(sinx+cosx)在区间[0,
ex(sinx+cosx)在区间[0, ]上的值域为( )
]上的值域为( )
A.[ ,
, e
e ] B.(
] B.( ,
, e
e ) C.[1,e
) C.[1,e ] D.(1,e
] D.(1,e )
)
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:解答题
设A、B、C是半径为1的球面上的三点,B、C两点间的球面距离为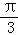 ,点A与B、C两点间的球面距离均为
,点A与B、C两点间的球面距离均为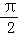 ,O为球心,
,O为球心,
求:(1)∠AOB、∠BOC的大小;
(2)球心O到截面ABC的距离.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
设f(x)=sinxcosx,那么f′(x)=( )
A.﹣cosxsinx B.cos2x C.sinx+cosx D.cosx﹣sinx
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
(2012•桂林模拟)设a∈R,函数f(x)=ex+a•e﹣x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.ln2 B.﹣ln2 C.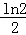 D.
D.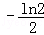
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
已知函数f(x)=x+lnx,则f′(1)的值为( )
A.1 B.2 C.﹣1 D.﹣2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
(2012•九江一模)已知f(x)是定义在(0,+∞)上的单调函数,且对任意的x∈(0,+∞),都有f[f(x)﹣x3]=2,则方程f(x)﹣f′(x)=2的解所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
若平面α的法向量为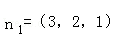 ,平面β的法向量为
,平面β的法向量为 ,则平面α与β夹角(锐角)的余弦是( )
,则平面α与β夹角(锐角)的余弦是( )
A.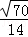 B.
B.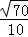 C.
C.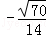 D.﹣
D.﹣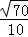
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
(2014•合肥二模)已知正方体ABCD﹣A1B1C1D1中,线段B1A1,B1C1上(不包括端点)各有一点P,Q,且B1P=B1Q,下列说法中,不正确的是( )
A.A,C,P,Q四点共面
B.直线PQ与平面BCC1B1所成的角为定值
C.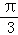 <∠PAC<
<∠PAC<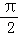
D.设二面角P﹣AC﹣B的大小为θ,则tanθ的最小值为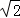
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:填空题
二项式 的展开式中含
的展开式中含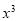 的项的系数是__________.(用数字作答)
的项的系数是__________.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com