
【题目】已知函数f(x)是定义在R上的奇函数,且f(x)的图象关于直线x=1对称.
(1)求证:f(x)是周期为4的周期函数;
(2)若f(x)= ![]() (0<x≤1),求x∈[﹣5,﹣4]时,函数f(x)的解析式.
(0<x≤1),求x∈[﹣5,﹣4]时,函数f(x)的解析式.
【答案】
(1)证明:由函数f(x)的图象关于直线x=1对称,
有f(x+1)=f(1﹣x),即有f(﹣x)=f(x+2).
又函数f(x)是定义在R上的奇函数,故有f(﹣x)=﹣f(x).
故f(x+2)=﹣f(x),从而f(x+4)=﹣f(x+2)=f(x),
即f(x)是周期为4的周期函数
(2)解:由函数f (x)是定义在R上的奇函数,可知f(0)=0.
x∈[﹣1,0)时,﹣x∈(0,1],f(x)=﹣f(﹣x)=﹣ ![]() .
.
故x∈[﹣1,0]时,f(x)=﹣ ![]() .
.
x∈[﹣5,﹣4]时,x+4∈[﹣1,0],f(x)=f(x+4)=﹣ ![]() .
.
从而,x∈[﹣5,﹣4]时,函数f(x)的解析式为f(x)=﹣ ![]()
【解析】(1)由题意图象关于直线x=1对称,得出f(﹣x)=f(x+2),再根据函数的奇偶性得到f(x+2)=﹣f(x)进而f(x+4)=f(x)故得到周期。(2)当x∈[﹣1,0)时,﹣x∈(0,1],由函数的奇偶性得到f(x)=﹣f(﹣x)=-![]() ,再根据函数的周期性得出x∈[﹣5,﹣4]时的函数f(x)的解析式。
,再根据函数的周期性得出x∈[﹣5,﹣4]时的函数f(x)的解析式。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图为函数y=f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分,其中点 ![]() 是图象的一个最高点,点
是图象的一个最高点,点 ![]() 是与点P相邻的图象与x轴的一个交点.
是与点P相邻的图象与x轴的一个交点.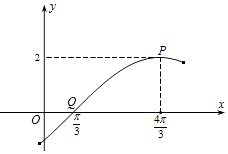
(1)求函数f(x)的解析式;
(2)若将函数f(x)的图象沿x轴向右平移 ![]() 个单位,再把所得图象上每一点的横坐标都变为原来的
个单位,再把所得图象上每一点的横坐标都变为原来的 ![]() (纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
(纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 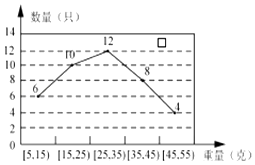
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() +cx+d有极值.
+cx+d有极值.
(Ⅰ)求实数c的取值范围;
(Ⅱ)若f(x)在x=2处取得极值,且当x<0时,f(x)< ![]() +2d恒成立,求实数d的取值范围.
+2d恒成立,求实数d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x= ![]() 时,函数f(x)取得最小值,则下列结论正确的是( )
时,函数f(x)取得最小值,则下列结论正确的是( )
A.f(2)<f(﹣2)<f(0)
B.f(0)<f(2)<f(﹣2)
C.f(﹣2)<f(0)<f(2)
D.f(2)<f(0)<f(﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx﹣cos2x﹣
sinxcosx﹣cos2x﹣ ![]() .
.
(Ⅰ)求函数f(x)的对称轴方程;
(Ⅱ)将函数f(x)的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移 ![]() 个单位,得到函数g(x)的图象.若a,b,c分别是△ABC三个内角A,B,C的对边,a=2,c=4,且g(B)=0,求b的值.
个单位,得到函数g(x)的图象.若a,b,c分别是△ABC三个内角A,B,C的对边,a=2,c=4,且g(B)=0,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 设方程f(x)=2﹣x+b(b∈R)的四个实根从小到大依次为x1 , x2 , x3 , x4 , 对于满足条件的任意一组实根,下列判断中一定成立的是( )
设方程f(x)=2﹣x+b(b∈R)的四个实根从小到大依次为x1 , x2 , x3 , x4 , 对于满足条件的任意一组实根,下列判断中一定成立的是( )
A.x1+x2=2
B.e2<x3x4<(2e﹣1)2
C.0<(2e﹣x3)(2e﹣x4)<1
D.1<x1x2<e2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com