【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且满足 
+ 
=4cosC． （Ⅰ）求 
的值；
（Ⅱ）若tanA=2tanB，求sinA的值．
【答案】解：（Ⅰ）已知等式整理得： 
=4cosC，即 
=2abcosC， 由余弦定理得：c2=a2+b2﹣2abcosC=a2+b2﹣ = ，
即 
=2，
利用正弦定理化简得： 
= =2；
（Ⅱ）∵tanA=2tanB，
∴ 
，则sinAcosB=2sinBcosA，
∴a 
=2b 
，
化简得，3a2﹣3b2=c2 ，
联立a2+b2=2c2得，a 
、 
，
由余弦定理得，cosA= = 
= 
，
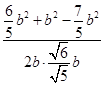由0＜A＜π得，sinA= 
．
【解析】（Ⅰ）根据余弦定理和正弦定理化简已知的式子，即可求出式子的值；（Ⅱ）利用商的关系化简tanA=2tanB，再根据余弦定理和正弦定理化简得到等式，联立（1）的结论求出a、b、c的关系，利用余弦定理求出cosA，再由内角的范围和平方关系求出sinA的值．
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】2003年至2015年北京市电影放映场次（单位：万次）的情况如图所示，下列函数模型中，最不适合近似描述这13年间电影放映场次逐年变化规律的是（ ）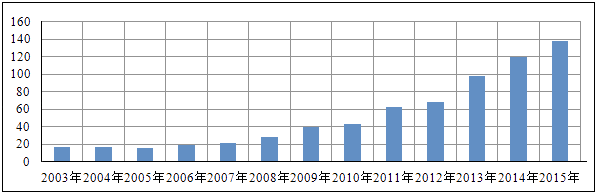
A.f（x）=ax2+bx+c
B.f（x）=aex+b
C.f（x）=eax+b
D.f（x）=alnx+b
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2，M是PD的中点． 
（1）求证：平面ABM⊥平面PCD；
（2）求直线CD与平面ACM所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}满足：a1=1，an+1+（﹣1）nan=2n﹣1．
（1）求a2 ， a4 ， a6；
（2）设bn=a2n ， 求数列{bn}的通项公式；
（3）设Sn为数列{an}的前n项和，求S2018 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱锥P﹣ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=AB=4，∠CDA=120°，点N在线段PB上，且PN= 
．
（Ⅰ）求证：BD⊥PC；
（Ⅱ）求证：MN∥平面PDC；
（Ⅲ）求二面角A﹣PC﹣B的余弦值．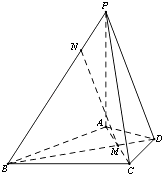
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
