
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]() 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.

(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ) (1)![]() ,(2)
,(2)![]() .
.
【解析】试题分析:(Ⅰ)利用中位线定理得出DE//AB,即可证得;
(Ⅱ)(1)在![]() 中,利用勾股定理运算即可;
中,利用勾股定理运算即可;
(2)以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系,利用向量求解线面角即可.
试题解析:
(Ⅰ)证明:连结![]() 交
交![]() 于E,连结DE,
于E,连结DE,
∵D、E分别为![]() 和
和![]() 的中点,
的中点,
∴DE//AB,
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴AB//平面CDB1;
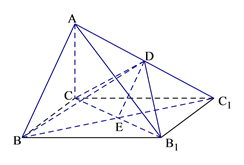
(Ⅱ)(1)∵AC⊥平面BCC1B1, ![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
在![]() ,∵BC=1,
,∵BC=1, ![]() ,
,
∴![]() ;
;
【注:以上加灰色底纹的条件不写不扣分!】
(2)依题意知AC、BC、CC1两两互相垂直,以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系如图示,
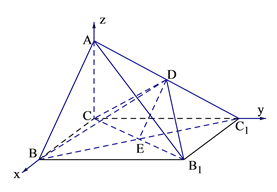
易得![]() ,
, ![]() ,
,
![]() ,
, 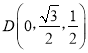 ,
,
故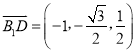 ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() 得
得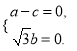 令
令![]() 得
得![]() ,
,
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则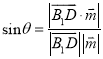
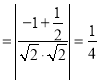 ,
,
即![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
【其它解法请参照给分,如先用体积法求出点D到平面ABB1的距离![]() ,(10分)再用公式
,(10分)再用公式![]() 算
算![]() 与平面
与平面![]() 所成角的正弦值(12分)】
所成角的正弦值(12分)】


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】若数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将数列
,则将数列![]() 和
和![]() 的距离定义为
的距离定义为![]() .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,数列
的集合,数列![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() .若
.若![]() ,
, ![]() ,数列
,数列![]() 和
和![]() 的距离小于2016,求
的距离小于2016,求![]() 的最大值.
的最大值.
(3)记![]() 是所有7项数列
是所有7项数列![]() (其中
(其中![]() ,
, ![]() 或
或![]() )的集合,
)的集合, ![]() ,且
,且![]() 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: ![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,给出四个结论:
,给出四个结论:
①函数![]() 是最小正周期为
是最小正周期为![]() 的奇函数;
的奇函数;
②函数![]() 的图像的一条对称轴是
的图像的一条对称轴是![]() ;
;
③函数![]() 图像的一个对称中心是
图像的一个对称中心是![]() ;
;
④函数![]() 的递增区间为
的递增区间为![]() .则正确结论的个数为( )
.则正确结论的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点
的焦点![]() 重合,且点
重合,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
, ![]() 与
与![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() .沿
.沿![]() 将
将![]() 折起,使
折起,使![]() 至
至![]() 处,且
处,且![]() ;然后再将
;然后再将![]() 沿
沿![]() 折起,使
折起,使![]() 至
至![]() 处,且面
处,且面![]() 面
面![]() ,
,![]() 和
和![]() 在面
在面![]() 的同侧.
的同侧.

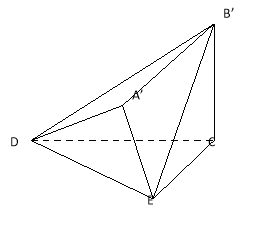
(Ⅰ) 求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求平面![]() 与平面
与平面![]() 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(![]() ,表示丢失的数据)
,表示丢失的数据)
无意愿 | 有意愿 | 总计 | |
男 |
|
| 40 |
女 | 5 |
|
|
总计 | 25 |
| 80 |
(1)求出![]() 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
(2)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据: 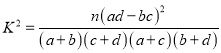 ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市英才中学的一个社会实践调查小组,在对中学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对收回的120份有效问卷进行统计,得到如下![]() 列联表:
列联表:
做不到光盘 | 能做到光盘 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现已按是否能做到光盘分层从45份女生问卷中抽取9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过![]() ,那么根据临界值表最精确的
,那么根据临界值表最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量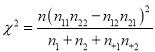 ,其中
,其中![]() .
.
独立性检验临界表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com