练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直角梯形中，是边长为2的等边三角形，．沿将折起，使至处，且；然后再将沿折起，使至处，且面面，和在面的同侧．

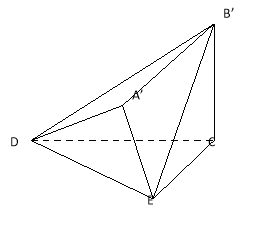
    (Ⅰ) 求证：平面；

    (Ⅱ) 求平面与平面所构成的锐二面角的余弦值．

    【答案】(Ⅰ) 详见解析；(Ⅱ ) 平面与平面所构成的锐二面角的余弦值为．

    【解析】

    试题分析：(Ⅰ) 在直角梯形ABCD中，由平面几何知识，又，可证得平面；(Ⅱ ) 建立空间直角坐标系，利用法向量可求出二面角的余弦值．

    试题解析：(Ⅰ)证明：在直角梯形ABCD中，可算得

    根据勾股定理可得，即：，又，平面；

    (Ⅱ) 以C为原点，CE为y轴，CB为z轴建立空间直角坐标系，如图，则,，，，作，因为面面，易知，，且，

    从平面图形中可知：，易知面CDE的法向量为

    设面PAD的法向量为，且．

    解得

    故所求平面与平面所构成的锐二面角的余弦值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2017年五一假期期间，高速公路车辆较多。某调査公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调 査，将他们在某段高速公路的车速分成六段： 后得到如图的频率分布直方图.

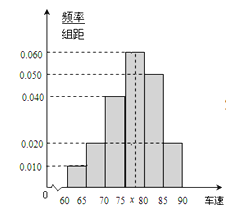
    （Ⅰ）求这40辆小型车辆车速的众数和中位数以及平均数的估计值.

    （Ⅱ）若从车速在的车辆中任抽取2辆，求车速在的车辆恰有一辆的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高中在校学生2 000人，高一年级与高二年级人数相同并且都比高三年级多1人．为了响应市教育局“阳光体育”号召，该校开展了跑步和跳绳两项比赛，要求每人都参加而且只参加其中一项，各年级参与项目人数情况如下表：

    　　年级

    项目　　

    高一年级

    高二年级

    高三年级

    跑步

    a

    b

    c

    跳绳

    x

    y

    z

    其中a∶b∶c＝2∶3∶5，全校参与跳绳的人数占总人数的. 为了了解学生对本次活动的满意度，采用分层抽样从中抽取一个200人的样本进行调查，则高二年级中参与跑步的同学应抽取多少人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线的参数方程为（为参数），在以原点为极点， 轴正半轴为极轴的极坐标系中，直线的极坐标方程为.

    （1）求的普通方程和的倾斜角；

    （2）设点， 和交于两点，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥的底面为矩形，D为的中点，AC⊥平面BCC1B1．

    （Ⅰ）证明：AB//平面CDB1;

    （Ⅱ）若AC=BC=1，BB1=,

    （1）求BD的长；

    （2）求B1D与平面ABB1所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为的函数是奇函数.

    （1）求的值；

    （2）证明： 为上的增函数；

    （3）若对任意的，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

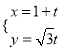    已知曲线的极坐标方程是，以极点为原点，极轴为轴的正半轴建立平面直角坐标系，直线的参数方程为（为参数）.

    （Ⅰ）写出直线的普通方程与曲线的直角坐标方程；

    （Ⅱ）设曲线经过伸缩变换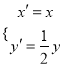得到曲线，若点，直线与交与， ，求， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）.

    （Ⅰ）若曲线在点处的切线与轴垂直，求的值；

    （Ⅱ）若函数有两个极值点，求的取值范围；

    （Ⅲ）证明：当时， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】海州市六一儿童节期间在妇女儿童活动中心举行小学生“海州杯”围棋比赛，规则如下：甲、乙两名选手比赛时，每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或赛满6局时比赛结束.设某校选手甲与另一选手乙比赛时，甲每局获胜的概率皆为，且各局比赛胜负互不影响，已知第二局比赛结束时比赛停止的概率为.

    (1)求的值；

    (2)设表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案