
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)证明: ![]() 为
为![]() 上的增函数;
上的增函数;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ; (2)见解析;(3)
; (2)见解析;(3)![]() .
.
【解析】试题分析:(1)根据奇函数的定义,取x=1,得f(1)+f(﹣1)=0,解之得a=2,再经过检验可得当a=2时,f(x)+f(﹣x)=0对x∈R恒成立,所以f(x)是奇函数;(2)令t=2x,得![]() ,再用单调性的定义,证出当x1∈R,x2∈R且x1<x2时,y1﹣y2=
,再用单调性的定义,证出当x1∈R,x2∈R且x1<x2时,y1﹣y2=![]() ,讨论可得y1<y2,所以f(x)在R上是增函数;(3)因为f(x)是奇函数,并且在R上是增函数,所以原不等式对任意的x∈R恒成立,即mx2+1>mx﹣1对任意的x∈R恒成立,化简整理得关于m的一元二次不等式,最后经过分类讨论,可得实数m的取值范围为0≤m<8.
,讨论可得y1<y2,所以f(x)在R上是增函数;(3)因为f(x)是奇函数,并且在R上是增函数,所以原不等式对任意的x∈R恒成立,即mx2+1>mx﹣1对任意的x∈R恒成立,化简整理得关于m的一元二次不等式,最后经过分类讨论,可得实数m的取值范围为0≤m<8.
试题解析:
(1)∵函数是奇函数,
∴![]() ,
,
可得 ,解之得:
,解之得: ![]() ,
,
检验: ![]() 时,
时, ![]() ,
,
∴
∴![]() 对
对![]() 恒成立,即
恒成立,即![]() 是奇函数.
是奇函数.
∴![]()
(2)证明:令![]() ,则
,则![]()
![]()
![]()
![]()
设![]() ,
, ![]() ,且
,且![]() ,∵
,∵![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() ,
,
当![]() 时,∴
时,∴ ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,可得
,可得![]() 在
在![]() 上是增函数.
上是增函数.
(3)∵![]() 是奇函数,
是奇函数,
∴不等式![]() 等价于
等价于![]()
∵![]() 在
在![]() 上是增函数,
上是增函数,
∴对任意的![]() ,原不等式恒成立,即
,原不等式恒成立,即![]() 对任意
对任意![]() 恒成立,
恒成立,
化简整理得: ![]() 对任意
对任意![]() 恒成立,
恒成立,
(1)当![]() 时,不等式即为
时,不等式即为![]() 恒成立,符合题意;
恒成立,符合题意;
(2)当![]() 时,有
时,有![]() ,即
,即![]() ,
,
综上所述:可得实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】设命题![]() 是
是![]() 的必要而不充分条件;
的必要而不充分条件;
设命题![]() 实数
实数![]() 满足方程
满足方程![]() 表示双曲线.
表示双曲线.
(1)若“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 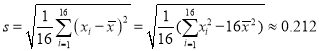 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() .沿
.沿![]() 将
将![]() 折起,使
折起,使![]() 至
至![]() 处,且
处,且![]() ;然后再将
;然后再将![]() 沿
沿![]() 折起,使
折起,使![]() 至
至![]() 处,且面
处,且面![]() 面
面![]() ,
,![]() 和
和![]() 在面
在面![]() 的同侧.
的同侧.

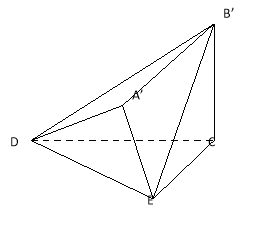
(Ⅰ) 求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求平面![]() 与平面
与平面![]() 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)用定义证明函数![]() 在
在![]() 上是增函数;
上是增函数;
(2)探究是否存在实数![]() ,使得函数
,使得函数![]() 为奇函数?若存在,求出
为奇函数?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)在(2)的条件下,解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
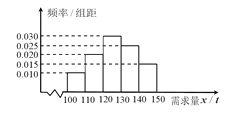
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语文成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
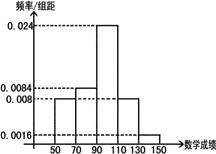
(Ⅰ)如果成绩大于135的为特别优秀,这500名学生中本次考试语文、数学特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布的)
(Ⅱ)如果语文和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附参考公式)若![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线
的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线![]() 与椭圆
与椭圆![]() 有且仅有一个交点
有且仅有一个交点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与
与![]() 轴交于
轴交于![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于两不同点
交于两不同点![]() ,
, ![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com