
如图,已知正方形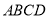 的边长为
的边长为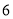 ,点
,点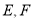 分别在边
分别在边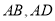 上,
上,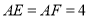 ,现将△
,现将△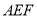 沿线段
沿线段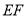 折起到△
折起到△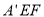 位置,使得
位置,使得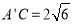 .
.
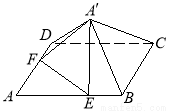
(1)求五棱锥 的体积;
的体积;
(2)在线段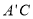 上是否存在一点
上是否存在一点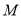 ,使得
,使得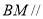 平面
平面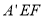 ?若存在,求
?若存在,求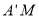 ;若不存在,说明理由.
;若不存在,说明理由.
(1)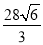 ;(2)
;(2)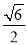
【解析】
试题分析:(1)由于△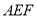 沿线段
沿线段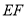 折起到△
折起到△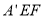 的过程中,平面
的过程中,平面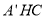
 平面
平面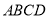 始终成立.所以
始终成立.所以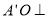 平面
平面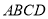 .又因为
.又因为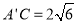 ,正方形
,正方形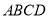 的边长为
的边长为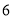 ,点
,点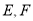 分别在边
分别在边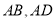 上,
上,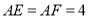 .即可求得结论.
.即可求得结论.
(2)因为线段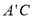 上是否存在一点
上是否存在一点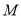 ,使得
,使得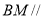 平面
平面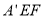 ,即相当于过点B作一个平面平行于平面
,即相当于过点B作一个平面平行于平面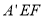 .故只需OM平行于
.故只需OM平行于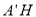 即可.
即可.

试题解析:(1)连接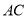 ,设
,设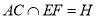 ,
,
由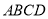 是正方形,
是正方形, ,
,
得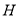 是
是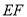 的中点,且
的中点,且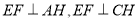 ,从而有
,从而有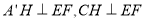 ,
,
所以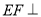 平面
平面 ,从而平面
,从而平面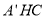
 平面
平面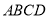 , 2分
, 2分
过点 作
作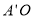 垂直
垂直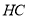 且与
且与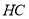 相交于点
相交于点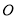 ,则
,则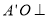 平面
平面 3分
3分
因为正方形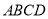 的边长为
的边长为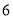 ,
,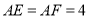 ,
,
得到: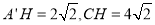 ,
,
所以 ,
,
所以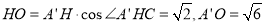
所以五棱锥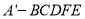 的体积
的体积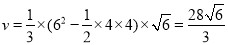 ; 6分
; 6分
(2)线段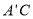 上存在点
上存在点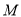 ,使得
,使得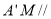 平面
平面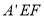 ,
,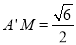 . 7分
. 7分
证明: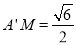
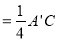 ,
, ,
,
所以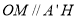 ,所以
,所以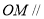 平面
平面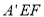 , 9分
, 9分
又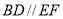 ,所以
,所以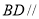 平面
平面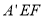 , 10分
, 10分
所以平面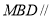 平面
平面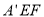 , 11分
, 11分
由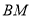 在平面
在平面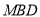 内,所以
内,所以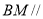 平面
平面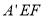 . 12分
. 12分
考点:1.线面垂直.2.面面垂直.3.五棱锥的体积.4.线面平行与面面平行.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟文科数学试卷(解析版) 题型:选择题
已知数列{an}的通项公式为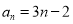 (n∈N+),则a3+a6 +a9+a12+a15=( )
(n∈N+),则a3+a6 +a9+a12+a15=( )
A.120 B.125 C.130 D.135
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
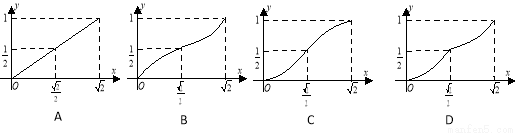
如图:正方体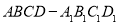 的棱长为
的棱长为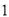 ,
,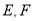 分别是棱
分别是棱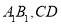 的中点,点
的中点,点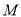 是
是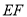 的动点,
的动点,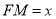 ,过点
,过点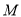 、直线
、直线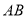 的平面将正方体分成上下两部分,记下面那部分的体积为
的平面将正方体分成上下两部分,记下面那部分的体积为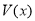 ,则函数
,则函数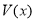 的大致图像是( )
的大致图像是( )
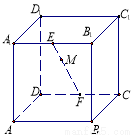
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
方程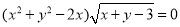 表示的曲线是( )
表示的曲线是( )
A.一个圆和一条直线 B.一个圆和一条射线C.一个圆 D.一条直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com