等差数列{an}中,a4=5,且a3,a6,a10成等比数列.
(1)求数列{an}的通项公式;
(2)写出数列{an}的前10项的和S10.
解:(1)设数列{a
n}的公差为d,则
a
3=a
4-d=5-d,a
6=a
4+2d=5+2d,a
10=a
4+6d=5+6d,
由a
3,a
6,a
10成等比数列得a
62=a
3 a
10,
即(5+2d)
2=(5-d)( 5+6d),
整理得10d
2-5d=0,解得d=0,或d=

.
当d=0时,a
4=a
1=5,a
n=5;
当
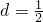
时,
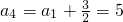
,
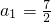
,
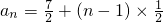
=
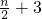
.
(2)当d=0时,
S
10=10•a
4=50.
当d=

时,
a
1=a
4-3d=5-

=

,
S
10=10×

+
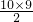
×

=

.
分析:(1)设数列{a
n}的公差为d,由a
3,a
6,a
10成等比数列得(5+2d)
2=(5-d)(5+6d),解得d=0,或d=

.由此能求出数列{a
n}的通项公式.
(2)当d=0时,S
10=10•a
4=50.当d=

时,a
1=a
4-3d=5-

=

,S
10=10×

+
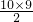
×

=

.
点评:本题考查等差数列的通项公式和前n项和公式的求法,解题时要认真审题,注意等比数列的性质的灵活运用.

 .
.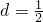 时,
时,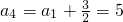 ,
,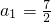 ,
,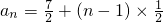 =
=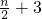 .
. 时,
时, =
= ,
, +
+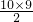 ×
× =
= .
. .由此能求出数列{an}的通项公式.
.由此能求出数列{an}的通项公式. 时,a1=a4-3d=5-
时,a1=a4-3d=5- =
= ,S10=10×
,S10=10× +
+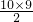 ×
× =
= .
.

 应用题作业本系列答案
应用题作业本系列答案