
分析 (I)利用递推关系与等比数列的定义即可证明.
(II)利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(Ⅰ)当n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2),可得:an=2an-1.
当n=1时,a1=S=2a1-2,解得a1=2.
由等比数列的定义知,数列{an}是首项为2,公比为2的等比数列,
∴an=2n.
(Ⅱ)证明:bn=log2an=n.
${c_n}=\frac{b_n}{a_n}$=$\frac{n}{{2}^{n}}$,
∴Tn=$\frac{1}{2}+\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,①
以上等式两边同乘以$\frac{1}{2}$,得$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n}}$+$\frac{n}{{2}^{n+1}}$,②
①-②,得$\frac{1}{2}{T}_{n}$=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$=$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$=1-$(\frac{1}{2})^{n}$-$\frac{n}{{2}^{n+1}}$=1-$\frac{n+2}{{2}^{n}}$,
∴Tn=2-$\frac{n+2}{{2}^{n}}$<2.
点评 本题考查了等比数列的通项公式与求和公式、数列递推关系、“错位相减法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{8}{3}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{1}{2}$ | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
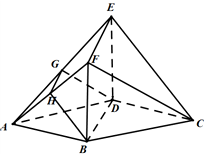 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=2,G和H分别是AE和AF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=2,G和H分别是AE和AF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
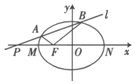 如图,设F(-c,0)是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点,点P(-$\frac{{a}^{2}}{c}$,0)是x轴上的一点,点M,N为椭圆的左、右顶点,已知|MN|=8,且|PM|=2|MF|
如图,设F(-c,0)是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点,点P(-$\frac{{a}^{2}}{c}$,0)是x轴上的一点,点M,N为椭圆的左、右顶点,已知|MN|=8,且|PM|=2|MF|查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0),(1,0) | B. | (0,-6),(0,6) | C. | (-6,0),(6,0) | D. | $(-\sqrt{6},0),(\sqrt{6},0)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com