
【题目】极坐标系与直角坐标系xoy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为 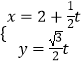 (t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ. (I)求C的直角坐标方程;
(t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ. (I)求C的直角坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求弦长|AB|.
科目:高中数学 来源: 题型:
【题目】已知非空集合A,B满足以下两个条件.
(ⅰ)A∪B={1,2,3,4,5,6},A∩B=;
(ⅱ)A的元素个数不是A中的元素,B的元素个数不是B中的元素,则有序集合对(A,B)的个数为( )
A.10
B.12
C.14
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD. 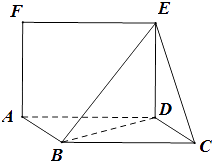
(Ⅰ)求证:BD⊥平面ECD.
(Ⅱ)求D点到面CEB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法: ①函数y=﹣cos2x的最小正周期是π;
②终边在y轴上的角的集合是{α|α= ![]() ,k∈Z};
,k∈Z};
③在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④函数f(x)=4sin(2x+ ![]() )(x∈R)可以改写为y=4cos(2x﹣
)(x∈R)可以改写为y=4cos(2x﹣ ![]() );
);
⑤函数y=sin(x﹣ ![]() )在[0,π]上是减函数.
)在[0,π]上是减函数.
其中,正确的说法是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种机器的固定成本为5000元,且每生产100部,需要加大投入2500元.对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入函数为 ![]() ,其中x是产品售出的数量0≤x≤500.
,其中x是产品售出的数量0≤x≤500.
(1)若为x年产量,y表示利润,求y=f(x)的解析式
(2)当年产量为何值时,工厂的年利润最大?其最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() .
.
(1)求f(x)的周期及其图象的对称中心;
(2)△ABC中,角A、B、C所对的边分别是a、b、c,满足(2a﹣c)cosB=bcosC,求f(B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,A={x|2x2﹣9x+4≤0},B={x|x2+a<0}.
(1)当a=﹣9时,求A∩B,(RA)∪B;
(2)当a<0时,若(RA)∩B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 为奇函数.
为奇函数.
(1)若函数f(x)在区间 ![]() 上为单调函数,求m的取值范围;
上为单调函数,求m的取值范围;
(2)若函数f(x)在区间[1,k]上的最小值为3k,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)= ![]() (a>0且a≠1)
(a>0且a≠1)
(1)若a=2,解不等式f(x)≤5;
(2)若函数f(x)的值域是[4,+∞),求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com