练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】中国文化中有很多东西喜欢9或9的倍数.如：九连环、九阴白骨爪、降龙十八掌（）、三十六计（）、孙悟空七十二变（）、八十一难（）等.若一个三位数的各位数字之和为9，如207，126，则这样的三位数共有________.

    【答案】

    【解析】

    根据三位数的各位数字之和为9,列举出所有符合要求的三位数即可.

    三位数的各位数字之和为9,符合要求的三位数如下所示:

    108,117,126,135,144,153,162,171,180,

    207,216,225,234,243,252,261,270,

    306,315,324,333,342,351,360,

    405,414,423,432,441,450,

    504,513,522,531,540

    603,612,621,630

    702,711,720,

    801,810,

    900,

    由以上可知符合各位数字之和为9的三位数共有45个

    故答案为:45

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】福利彩票“双色球”中红球的号码可以从01，02，03，…，32，33这33个二位号码中选取，小明利用如图所示的随机数表选取红色球的6个号码，选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字，则第四个被选中的红色球号码为（ ）

    81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85

    06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49

    A. 12 B. 33 C. 06 D. 16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了检验学习情况，某培训机构于近期举办一场竞赛活动，分别从甲、乙两班各抽取10名学员的成绩进行统计分析，其成绩的茎叶图如图所示（单位：分），假设成绩不低于90分者命名为“优秀学员”.

    （1）分别求甲、乙两班学员成绩的平均分（结果保留一位小数）；

    （2）从甲班4名优秀学员中抽取两人，从乙班2名80分以下的学员中抽取一人，求三人平均分不低于90分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，平面，，.

    （Ⅰ）求证：平面；

    （Ⅱ）求直线与平面所成角的正弦值；

    （Ⅲ）若二面角的余弦值为，求线段的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：，直线：，：

    （1）若，，被圆C所截得的弦的长度之比为，求实数k的值

    （2）已知线段AB的端点B的坐标是，端点A在圆C上运动，求线段AB的中点M的轨迹方程

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中设倾斜角为的直线的参数方程为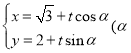为参数）．在以坐标原点为极点，以轴正半轴为极轴建立的极坐标系中，曲线的极坐标方程为，直线与曲线相交于不同的两点．

    （1）若，求直线的普通方程和曲线的直角坐标方程；

    （2）若为与的等比中项，其中，求直线的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （Ⅰ）求的单调区间；

    （Ⅱ）当时，试判断零点的个数；

    （Ⅲ）当时，若对，都有（）成立，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数的图像向左平移个单位后得到函数的图像，且函数满足，则下列命题中正确的是（）

    A. 函数图像的两条相邻对称轴之间的距离为

    B. 函数图像关于点对称

    C. 函数图像关于直线对称

    D. 函数在区间内为单调递减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线过焦点且平行于轴的弦长为.点，直线与交于两点，

    （1）求抛物线的方程；

    （2）若不平行于轴，且为坐标原点），证明:直线过定点.

    查看答案和解析>>

    同步练习册答案