
【题目】已知圆C:![]() ,直线
,直线![]() :
:![]() ,
,![]() :
:![]()
(1)若![]() ,
,![]() ,被圆C所截得的弦的长度之比为
,被圆C所截得的弦的长度之比为![]() ,求实数k的值
,求实数k的值
(2)已知线段AB的端点B的坐标是![]() ,端点A在圆C上运动,求线段AB的中点M的轨迹方程
,端点A在圆C上运动,求线段AB的中点M的轨迹方程
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为3的正方形,
是边长为3的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,BE与平面
,BE与平面![]() 所成角为
所成角为![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设点M在线段BD上,且![]() 平面BEF,求
平面BEF,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为y=![]() x-2
x-2![]() ,又直线l过椭圆C:
,又直线l过椭圆C:![]() (a>b>0)的右焦点,且椭圆的离心率为
(a>b>0)的右焦点,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点D(0,1)的直线与椭圆C交于点A,B,求△AOB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 | 3 | 4 | 5 | 6 | 7 | 8 |
销量 | 70 | 65 | 62 | 59 | 56 |
|
已知![]() .
.
(1)若变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .当销售数据
.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从
称为一个“好数据”.现从![]() 个销售数据中任取
个销售数据中任取![]() 个,求“好数据”至少
个,求“好数据”至少![]() 个的概率.
个的概率.
(参考公式:线性回归方程中![]() ,
,![]() 的估计值分别为
的估计值分别为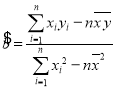 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国文化中有很多东西喜欢9或9的倍数.如:九连环、九阴白骨爪、降龙十八掌(![]() )、三十六计(
)、三十六计(![]() )、孙悟空七十二变(
)、孙悟空七十二变(![]() )、八十一难(
)、八十一难(![]() )等.若一个三位数的各位数字之和为9,如207,126,则这样的三位数共有________.
)等.若一个三位数的各位数字之和为9,如207,126,则这样的三位数共有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(1)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(2)若甲必选![]() ,记
,记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已经成为当下最热门的健身方式,小李的微信朋友圈内也有大量的好友参加了“微信运动”.他随机的选取了其中30人,记录了他们某一天走路的步数,将数据整理如下:
步数 |
|
|
|
人数 | 5 | 13 | 12 |
(1)若采用样本估计总体的方式,试估计小李所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数若超过8000步则他被系统评定为“积极型”,否则评定为“懈怠型”,将这30人按照“积极型”、“懈怠型”分成两层,进行分层抽样,从中抽取5人,将这5人中属于“积极型”的人依次记为![]() ,属于“懈怠型”的人依次记为
,属于“懈怠型”的人依次记为![]() ,现再从这5人中随机抽取2人接受问卷调查.设
,现再从这5人中随机抽取2人接受问卷调查.设![]() 为事件“抽取的2人来自不同的类型”,求事件
为事件“抽取的2人来自不同的类型”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com