
【题目】“微信运动”已经成为当下最热门的健身方式,小李的微信朋友圈内也有大量的好友参加了“微信运动”.他随机的选取了其中30人,记录了他们某一天走路的步数,将数据整理如下:
步数 |
|
|
|
人数 | 5 | 13 | 12 |
(1)若采用样本估计总体的方式,试估计小李所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数若超过8000步则他被系统评定为“积极型”,否则评定为“懈怠型”,将这30人按照“积极型”、“懈怠型”分成两层,进行分层抽样,从中抽取5人,将这5人中属于“积极型”的人依次记为![]() ,属于“懈怠型”的人依次记为
,属于“懈怠型”的人依次记为![]() ,现再从这5人中随机抽取2人接受问卷调查.设
,现再从这5人中随机抽取2人接受问卷调查.设![]() 为事件“抽取的2人来自不同的类型”,求事件
为事件“抽取的2人来自不同的类型”,求事件![]() 发生的概率.
发生的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据30人中一天走路步数超过5000步的有25人,由古典概型概率公式可得结果;(2)根据分层抽样方法可得,5人中“积极型”有![]() 人, “懈怠型”有
人, “懈怠型”有![]() 人,利用列举法可得,在这5人中任选2人,共10种不同的等可能结果:抽取的2人来自不同的类型”有6种不同的等可能结果,由古典概型概率公式可得结果.
人,利用列举法可得,在这5人中任选2人,共10种不同的等可能结果:抽取的2人来自不同的类型”有6种不同的等可能结果,由古典概型概率公式可得结果.
(1)由题意知30人中一天走路步数超过5000步的有25人,频率为![]() ,
,
![]() 估计小李所有微信好友中每日走路步数超过5000步的概率为
估计小李所有微信好友中每日走路步数超过5000步的概率为![]() .
.
(2)5人中“积极型”有![]() 人,这两人分别记为
人,这两人分别记为![]()
5人中“懈怠型”有![]() 人,这三人分别记为
人,这三人分别记为![]() .
.
在这5人中任选2人,共有以下10种不同的等可能结果:
![]() .
.
事件![]() “抽取的2人来自不同的类型”有以下6种不同的等可能结果:
“抽取的2人来自不同的类型”有以下6种不同的等可能结果:
![]() .
.
易得,其概率为![]() .
.
![]() 事件
事件![]() 发生的概率
发生的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆C:![]() ,直线
,直线![]() :
:![]() ,
,![]() :
:![]()
(1)若![]() ,
,![]() ,被圆C所截得的弦的长度之比为
,被圆C所截得的弦的长度之比为![]() ,求实数k的值
,求实数k的值
(2)已知线段AB的端点B的坐标是![]() ,端点A在圆C上运动,求线段AB的中点M的轨迹方程
,端点A在圆C上运动,求线段AB的中点M的轨迹方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
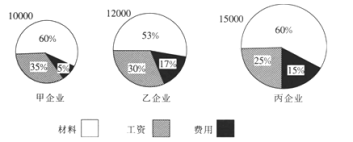
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)

(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解手机品牌的选择是否和年龄的大小有关,随机抽取部分华为手机使用者和苹果机使用者进行统计,统计结果如下表:
年龄 手机品牌 | 华为 | 苹果 | 合计 |
30岁以上 | 40 | 20 | 60 |
30岁以下(含30岁) | 15 | 25 | 40 |
合计 | 55 | 45 | 100 |
附:
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根据表格计算得![]() 的观测值
的观测值![]() ,据此判断下列结论正确的是( )
,据此判断下列结论正确的是( )
A.没有任何把握认为“手机品牌的选择与年龄大小有关”
B.可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”
C.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”
D.可以在犯错误的概率不超过0.01
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(Ⅰ)求![]() 的值
的值
(Ⅱ)设![]() ,若
,若![]() 的所有零点中,仅有两个大于
的所有零点中,仅有两个大于![]() ,设为
,设为![]() ,
,![]() (
(![]() )
)
(1)求证:![]() ,
,![]() .
.
(2)过点![]() ,
,![]() 的直线的斜率为
的直线的斜率为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com