数列{an}满足下列条件:a1=1,且对于任意的正整数n,恒有a2n=an+n,则a1024=( )
A.1023
B.1024
C.512
D.2048
【答案】
分析:直接由a
2n=a
n+n,可得a
1024=a
512+512=a
512+2
9=a
256+256+512=a
256+2
8+2
9=a
128+128+256+512=a
128+2
7+2
8+2
9=a
64+2
6+2
7+2
8+2
9=…=a
2+2
2+2
3+…+2
8+2
9=a
1+1+2
1+2
2+…+2
8+2
9=1+1+2
1+2
2+…+2
8+2
9,再代入等比数列的求和公式即可求得结论.
解答:解:因为对于任意的正整数n,恒有a
2n=a
n+n,
所以:a
1024=a
512+512=a
512+2
9=a
256+256+512=a
256+2
8+2
9=a
128+128+256=a
128+2
7+2
8+2
9=a
64+2
6+2
7+2
8+2
9=…
=a
2+2
2+2
3+…+2
8+2
9=a
1+1+2
1+2
2+…+2
8+2
9=1+1+2
1+2
2+…+2
8+2
9=1+
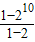
=1024.
故答案为1024.
点评:本题主要考查利用递推关系求数列中的特定项,在做这一类型题目时,一定要找到递推关系对应的规律,按规律解题.

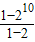 =1024.
=1024.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案