Question

已知直线l：x-y+3=0，一束光线从点A（1，2）处射向x轴上一点B，又从B点反射到l上一点C，最后又从C点反射回A点．
（Ⅰ）试判断由此得到的△ABC是有限个还是无限个？
（Ⅱ）依你的判断，认为是无限个时求出所以这样的△ABC的面积中的最小值；认为是有限个时求出这样的线段BC的方程．

Answer 1

分析：（Ⅰ）先设出B点坐标（m，0），根据对称点的特点得到A′和B′的坐标，表示出直线A′B的方程与直线l联立求出点C的横坐标，同理表示出直线AB′的方程与直线l联立求出点C的横坐标，两个相等求出m的值，经过判断得到三角形ABC的个数；
（Ⅱ）由m的值得到B和C的坐标，求出斜率，即可写出直线的方程．

解答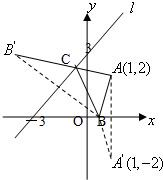：解：（Ⅰ）如图所示，
设B（m，0），点A关于x轴的对称点为A′（1，-2），点B关于直线l的对称点为B′（-3，m+3），根据光学性质，点C在直线A′B上，又在直线AB′上．
求得直线A′B的方程为y=

2

m-1

(x-m)，
由

y= 2 m-1 (x-m) y=x+3

解得xc=

3-5m

m-3

直线AB′的方程为y-2=

-m-1

4

(x-1)
由

y-2= -m-1 4 (x-1) y=x+3

解得xc=

m-3

m+5

，
则

3-5m

m-3

=

m-3

m+5

，得3m²+8m-3=0解得m=

1

3

或m=-3．
而当m=-3时，点B在直线l上，不能构成三角形，故这样的三角形只有一个．
（Ⅱ）当m=

1

3

时，B(

1

3

，0)， C(-

1

2

，

5

2

)，
∴线段BC的方程为3x+y-1=0(-

1

2

≤x≤

1

3

)．

点评：考查学生会求两条直线的交点坐标，会求点关于直线的对称点的坐标，会根据条件写出直线的一般方程．