
(本小题满分13分)设函数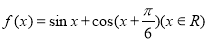
(1)求函数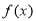 的最小正周期及其在区间
的最小正周期及其在区间 上的值域;
上的值域;
(2)记△ABC内角A,B,C的对边分别为a,b,c,若,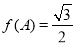 ,且
,且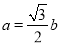 ,求角B的值.
,求角B的值.
(1) 的最小正周期为
的最小正周期为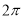 ,值域为
,值域为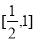 ;(2)
;(2)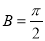 .
.
【解析】
试题分析:(1)将函数解析式第二项利用两角和与差的余弦函数公式及特殊角的三角函数值化简,合并整理后再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出 的值,代入周期公式即可求出
的值,代入周期公式即可求出 的最小正周期,再由
的最小正周期,再由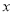 的范围,得出这个角的范围,利用正弦函数的图象与性质得出正弦函数的值域,即可得到
的范围,得出这个角的范围,利用正弦函数的图象与性质得出正弦函数的值域,即可得到 在区间
在区间 上的值域;
上的值域;
(2)由(1)得出的 解析式及
解析式及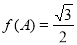 ,得出
,得出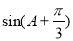 的值,利用特殊角的三角函数值求出
的值,利用特殊角的三角函数值求出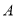 的度数,确定出
的度数,确定出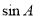 的值,再利正弦定理利用关系式,将已知的等式
的值,再利正弦定理利用关系式,将已知的等式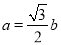 及
及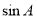 的值代入,求出
的值代入,求出 的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.
的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.
试题解析:(1)因为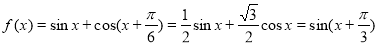 ,所以
,所以 的最小正周期为
的最小正周期为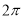 ;因为
;因为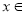
 ,所以
,所以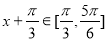 ,于是
,于是 ,所以函数
,所以函数 的值域为
的值域为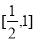 .
.
(2)由(1)可知, ,
, ,因为
,因为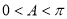 ,所以
,所以 ,所以
,所以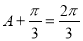 ,即
,即 .因为
.因为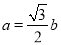 ,且
,且 ,所以
,所以
 ,又因为
,又因为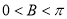 ,所以
,所以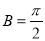 .
.
考点:正弦定理;三角函数中的恒等变换应用;三角函数的周期性及其求法;复合三角函数的单调性.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源:2015届西藏拉萨中学高三第三次月考文科数学试卷(解析版) 题型:解答题
(本小题12分)已知函数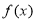 =
=
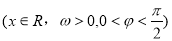 的部分图象如图所示。
的部分图象如图所示。
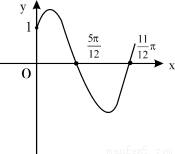
(1)求函数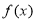 的解析式;
的解析式;
(2)求函数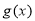 =
=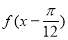 -
-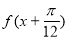 的单调递增区间。
的单调递增区间。
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检文科数学试卷(解析版) 题型:选择题
如果一个水平放置的图形的斜二侧直观图是一个底角为45°,腰和上底都为1的等腰梯形,那么原平面图形的面积是
A.2+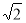 B.
B. C.
C.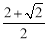 D.1+
D.1+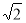
查看答案和解析>>
科目:高中数学 来源:2015届福建省高三10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系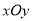 中,直线
中,直线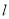 的参数方程为
的参数方程为 为参数),P、Q分别为直线
为参数),P、Q分别为直线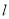 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线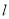 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,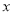 轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高三10月月考理科数学试卷(解析版) 题型:选择题
若函数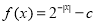 的图象与
的图象与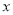 轴有公共点,则实数
轴有公共点,则实数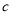 的取值范围为()
的取值范围为()
A.[一1,0) B.[0,1] C.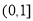 D.[1,+
D.[1,+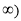
查看答案和解析>>
科目:高中数学 来源:2015届福建省、德化一中高三9月摸底考试理科数学试卷(解析版) 题型:填空题
某次测量发现一组数据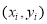 具有较强的相关性,并计算得
具有较强的相关性,并计算得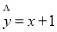 ,其中数据
,其中数据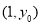 因书写不清,只记得
因书写不清,只记得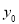 是
是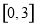 任意一个值,则该数据对应的残差的绝对值不大于1的概率为 .(残差=真实值-预测值.)
任意一个值,则该数据对应的残差的绝对值不大于1的概率为 .(残差=真实值-预测值.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com