
【题目】在△ABC中,a,b,c分别为A、B、C的对边,且满足2(a2﹣b2)=2accosB+bc
(1)求A
(2)D为边BC上一点,CD=3BD,∠DAC=90°,求tanB.
【答案】
(1)解:由题意2accosB=a2+c2﹣b2,
∴2(a2﹣b2)=a2+c2﹣b2+bc.
整理得a2=b2+c2+bc,
由余弦定理:a2=b2+c2﹣2bccosA
可得:bc=﹣2bccosA
∴cosA=﹣ ![]() ,
,
∵0<A<π
∴A= ![]() .
.
(2)解:∵∠DAC= ![]() ,
,
∴AD=CDsinC,∠DAB= ![]() .
.
在△ABD中,有 ![]() ,
,
又∵CD=3BD,
∴3sinC=2sinB,
由C= ![]() ﹣B,得
﹣B,得 ![]() cosB﹣
cosB﹣ ![]() sinB=2sinB,
sinB=2sinB,
整理得:tanB= ![]()
【解析】1、根据已知求得a2=b2+c2+bc,再利用余弦定理可得bc=﹣2bccosA,解得cosA的值,再由A的取值范围得到A的值。
2、由解三角形可得∠DAB= ![]() ,在△ABD中,根据正弦定理可得3sinC=2sinB,由C=
,在△ABD中,根据正弦定理可得3sinC=2sinB,由C= ![]() ﹣B,再利用两角和差的正弦公式展开,根据同角三角函数的基本公式可得结果。
﹣B,再利用两角和差的正弦公式展开,根据同角三角函数的基本公式可得结果。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2BC,E,F,E1分别是棱AA1 , BB1 , A1B1的中点. 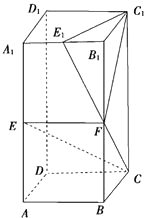
(1)求证:CE∥平面C1E1F;
(2)求证:平面C1E1F⊥平面CEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题“非空集合 ![]() 中的元素都是集合
中的元素都是集合 ![]() 中的元素”是假命题,
中的元素”是假命题,
那么下列命题中真命题的个数为( )
① ![]() 中的元素都不是
中的元素都不是 ![]() 中的元素 ②
中的元素 ② ![]() 中有不属于
中有不属于 ![]() 的元素
的元素
③ ![]() 中有属于
中有属于 ![]() 的元素 ④
的元素 ④ ![]() 中的元素不都是
中的元素不都是 ![]() 中的元素
中的元素
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 上的一点
上的一点 ![]() 的横坐标为
的横坐标为 ![]() ,焦点为
,焦点为 ![]() ,且
,且 ![]() ,直线
,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点.
两点.
(1)求抛物线 ![]() 的方程;
的方程;
(2)若 ![]() 是
是 ![]() 轴上一点,且△
轴上一点,且△ ![]() 的面积等于
的面积等于 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,我们的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题.某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产该型号空气净化器x(百台),其总成本为P(x)(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本).销售收入Q(x)(万元)满足Q(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
(1)求利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上函数f(x)是可导的,f(1)=2,且f(x)+f'(x)<1,则不等式f(x)﹣1<e1﹣x的解集是( )(注:e为自然对数的底数)
A.(1,+∞)
B.(﹣∞,0)∪(0,1)
C.(0,1)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足|x﹣1|>a其中a>0;命题q:实数x满足 ![]() <1
<1
(1)若命题p中a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,值域为
,值域为 ![]() ,如果存在函数
,如果存在函数 ![]() ,使得函数
,使得函数 ![]() 的值域仍是
的值域仍是 ![]() ,那么称
,那么称 ![]() 是函数
是函数 ![]() 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 ![]() 是不是函数
是不是函数 ![]() 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
① ![]() ;
;
② ![]() .
.
(2)设 ![]() 的定义域为
的定义域为 ![]() ,已知
,已知 ![]() 是
是 ![]() 的一个等值域变换,且函数
的一个等值域变换,且函数 ![]() 的定义域为
的定义域为 ![]() ,求实数
,求实数 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com