
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,值域为
,值域为 ![]() ,如果存在函数
,如果存在函数 ![]() ,使得函数
,使得函数 ![]() 的值域仍是
的值域仍是 ![]() ,那么称
,那么称 ![]() 是函数
是函数 ![]() 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 ![]() 是不是函数
是不是函数 ![]() 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
① ![]() ;
;
② ![]() .
.
(2)设 ![]() 的定义域为
的定义域为 ![]() ,已知
,已知 ![]() 是
是 ![]() 的一个等值域变换,且函数
的一个等值域变换,且函数 ![]() 的定义域为
的定义域为 ![]() ,求实数
,求实数 ![]() 的值.
的值.
【答案】
(1)解:① ![]() ,x>0,值域为R ,
,x>0,值域为R , ![]() ,t>0,由g(t)2可得y=f[g(t)]的值域为[1,+∞).
,t>0,由g(t)2可得y=f[g(t)]的值域为[1,+∞).
则x=g(t)不是函数y=f(x)的一个等值域变换;
② ![]() ,即
,即 ![]() 的值域为
的值域为 ![]() ,
,
当 ![]() 时,
时, ![]() ,即
,即 ![]() 的值域仍为
的值域仍为 ![]() ,所以
,所以 ![]() 是
是 ![]() 的一个等值域变换,故①不是等值域变换,②是等值域变换;
的一个等值域变换,故①不是等值域变换,②是等值域变换;
(2)解: ![]() 定义域为
定义域为 ![]() ,因为
,因为 ![]() 是
是 ![]() 的一个等值域变换,且函数
的一个等值域变换,且函数 ![]() 的定义域为
的定义域为 ![]() ,
, ![]() 的值域为
的值域为 ![]() ,
,![]() ,
,![]() 恒有
恒有 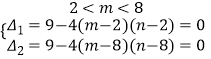 ,解得
,解得 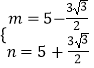 .
.
【解析】(1)在①中,函数 f ( x )的值域为R,函数y=f[g(t)]的值域为[1,+∞).所以①不是一个等值域变换。在②中f ( x ) 的值域为 [![]() , + ∞ ),y = f [ g ( t ) ] 的值域仍为 [,
, + ∞ ),y = f [ g ( t ) ] 的值域仍为 [,![]() , + ∞ ),所以①不是等值域变换,②是等值域变换。
, + ∞ ),所以①不是等值域变换,②是等值域变换。
(2)由题意可以得x = g ( t ) = ![]() , t ∈ R 的值域为 [ 2 , 8 ],通过2≤
, t ∈ R 的值域为 [ 2 , 8 ],通过2≤![]() ≤8 2 ( t 2 + 1 ) ≤ m t 2 3 t + n ≤ 8 ( t 2 + 1 ),可以求出m、n的值。
≤8 2 ( t 2 + 1 ) ≤ m t 2 3 t + n ≤ 8 ( t 2 + 1 ),可以求出m、n的值。
【考点精析】利用函数的定义域及其求法和函数的值域对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为A、B、C的对边,且满足2(a2﹣b2)=2accosB+bc
(1)求A
(2)D为边BC上一点,CD=3BD,∠DAC=90°,求tanB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①整数集可以表示为{x|x为全体整数}或{ ![]() };
};
②方程组 ![]() 的解集为 {x=3,y=1};
的解集为 {x=3,y=1};
③集合{x∈N|x2=1}用列举法可表示为{1,1};
④集合 ![]() 是无限集.
是无限集.
其中正确的是 ( )
A.①和③
B.②和④
C.④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x ![]() )﹣2sin(x
)﹣2sin(x ![]() )cos(x
)cos(x ![]() )
)
(1)求函数f(x)的最小正周期; (Ⅱ)求函数f(x)在区间[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项的和为Sn , 满足a1=0,an≥0,3an+12=an2+an+1(n∈N*) (Ⅰ)用数学归纳法证明:1 ![]() ≤an<1(n∈N*)
≤an<1(n∈N*)
(Ⅱ)求证:an<an+1(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个圆锥形的空杯子上放着一个直径为8cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?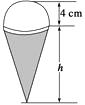
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 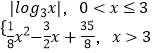 ,若函数g(x)=f(x)﹣m存在4个不同的零点x1 , x2 , x3 , x4 , 则实数m的取值范围是 , x1x2x3x4的取值范围是 .
,若函数g(x)=f(x)﹣m存在4个不同的零点x1 , x2 , x3 , x4 , 则实数m的取值范围是 , x1x2x3x4的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x焦点为F,点D为其准线与x轴的交点,过点F的直线l与抛物线相交于A,B两点,则△DAB的面积S的取值范围为( )
A.[5,+∞)
B.[2,+∞)
C.[4,+∞)
D.[2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知(2x﹣ ![]() )5(Ⅰ)求展开式中含
)5(Ⅰ)求展开式中含 ![]() 项的系数
项的系数
(Ⅱ)设(2x﹣ ![]() )5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
)5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com