
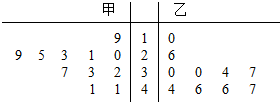
 ij���Ի���Ϊ�˽�����ڼס����������ֲͬһ������ij��������������ظ������ȡ��10�����磬�þ�Ҷͼ��ʾ������������߶ȵ����ݣ�������س�ȡ����ĸ߶ȵ�ƽ����$\overline{x}$����$\overrightarrow{x}$���ͷ�����бȽϣ����������ȷ���ǣ�������
ij���Ի���Ϊ�˽�����ڼס����������ֲͬһ������ij��������������ظ������ȡ��10�����磬�þ�Ҷͼ��ʾ������������߶ȵ����ݣ�������س�ȡ����ĸ߶ȵ�ƽ����$\overline{x}$����$\overrightarrow{x}$���ͷ�����бȽϣ����������ȷ���ǣ�������| A�� | $\overline{x}$����$\overrightarrow{x}$�����ҵ�����߶ȱȼ�����߶ȸ��ȶ� | |
| B�� | $\overline{x}$����$\overrightarrow{x}$����������߶ȱ��ҵ�����߶ȸ��ȶ� | |
| C�� | $\overline{x}$����$\overrightarrow{x}$�����ҵ�����߶ȱȼ�����߶ȸ��ȶ� | |
| D�� | $\overline{x}$����$\overrightarrow{x}$����������߶ȱ��ҵ�����߶ȸ��ȶ� |
���� ���ݾ�Ҷͼ������ס��ҵ�ƽ�������ٸ������ݵķֲ�����뷽��ĸ���ȽϿɵô𰸣�
��� �⣺���ݾ�Ҷͼ�У�
�ټ�����߶ȵ�ƽ����Ϊ$\overline{{x}_{��}}$=28cm��
�ҵ�����߶ȵ�ƽ����Ϊ$\overline{{x}_{��}}$=35cm��
�������߶ȵ�ƽ����С���ҵ�����ĸ߶ȵ�ƽ������
�ڼ�����߶ȷֲ���19��41֮�䣬�ҳɵ���ֲ����ұȽϼ�����ƽ�������ң�
�ҵ�����߶ȷֲ���10��47֮�䣬�������Եĵ���ֲ�����Է�ɢЩ��
�������߶����ҵ�����߶ȱȽϣ��������СЩ�����ȶ�Щ��
��ѡ��B��
���� ���⿼�������þ�Ҷͼ����ƽ�����뷽���Ӧ�����⣬�ؼ�����ȷ������Ҷͼ�����������ݣ��ǻ����⣮


 ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 0��1 | D�� | 0��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����f��x��=sin����x+�գ���$�أ�0��|��|��\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����ô��=2����=$\frac{��}{6}$��
��֪����f��x��=sin����x+�գ���$�أ�0��|��|��\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����ô��=2����=$\frac{��}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{24}$ | B�� | $\frac{1}{12}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com