
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: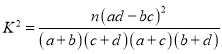 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
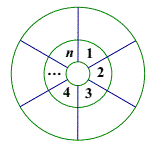
【题目】如图所示将同心圆环均匀分成n(![]() )格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
)格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
求甲在4局以内(含4局)赢得比赛的概率;
记![]() 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求![]() 的分布列和均值(数学期望).
的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会期间,甲、乙、丙三家中国企业都有意向购买同一种型号的机床设备,他们购买该机床设备的概率分别为![]() ,且三家企业的购买结果相互之间没有影响,则三家企业中恰有1家购买该机床设备的概率是
,且三家企业的购买结果相互之间没有影响,则三家企业中恰有1家购买该机床设备的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一张半径为1米的圆形铁皮,工人师傅需要剪一块顶角为锐角的等腰三角形![]() ,不妨设
,不妨设 ![]() ,
, ![]() 边上的高为
边上的高为 ![]() ,圆心为
,圆心为 ![]() ,为了使三角形的面积最大,我们设计了两种方案.
,为了使三角形的面积最大,我们设计了两种方案.

(1)方案1:设 ![]() 为
为 ![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积 ![]() ; 方案2:设
; 方案2:设![]() 的高
的高![]() 为
为![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积![]() ;
;
(2)请从(1)中的两种方案中选择一种,求出![]() 面积的最大值
面积的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com