
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
【答案】(1)极小值为![]() ;(2)
;(2)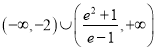
【解析】试题分析:(1)求出函数的导数,计算![]() 的值,求出
的值,求出![]() ,从而求出
,从而求出![]() 的单调区间,求出函数的极值即可;(2)令
的单调区间,求出函数的极值即可;(2)令![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() 的最小值,从而求出
的最小值,从而求出![]() 的范围即可.
的范围即可.
试题解析:(1)![]() (
(![]() ),因为曲线
),因为曲线![]() 在点(1,f(1))处的切线与直线
在点(1,f(1))处的切线与直线![]() 垂直,所以
垂直,所以![]() ,即
,即![]() ,解得
,解得![]() .所以
.所以![]() , ∴当
, ∴当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,f(x)在(2,+∞)上单调递增;∴当x=2时,f(x)取得极小值
,f(x)在(2,+∞)上单调递增;∴当x=2时,f(x)取得极小值![]() ,∴f(x)极小值为ln2.
,∴f(x)极小值为ln2.
(2)令![]() ,则
,则![]() ,欲使在区间上
,欲使在区间上![]() 上存在
上存在![]() ,使得
,使得![]() ,只需在区间
,只需在区间![]() 上
上![]() 的最小值小于零.令
的最小值小于零.令![]() 得,
得, ![]() 或
或![]() .当
.当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,解得
,解得![]() ,∵
,∵![]() ,∴
,∴![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]() 的最小值为
的最小值为![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,此时
,此时![]() 不成立.综上所述,实数m的取值范围为
不成立.综上所述,实数m的取值范围为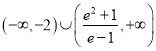


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线. 
(1)求∠BAE 的度数;
(2)求证: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,☉O内切于△ABC的边于点D,E,F,AB=AC,连接AD交☉O于点H,直线HF交BC的延长线于点G. 
(1)求证:圆心O在AD上;
(2)求证:CD=CG;
(3)若AH∶AF=3∶4,CG=10,求HF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d>0,其前n项和为Sn , 若S3=12,且2a1 , a2 , 1+a3成等比数列.
(1)求数列{an}的通项公式;
(2)记bn= ![]() (n∈N*),且数列{bn}的前n项和为Tn , 证明:
(n∈N*),且数列{bn}的前n项和为Tn , 证明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com