
已知向量 ,
,
 ,函数
,函数 的图象与直线
的图象与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
.
(1)求函数 在
在 上的单调递增区间;
上的单调递增区间;
(2)将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 在
在 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
科目:高中数学 来源: 题型:
随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表: 性别与读营养说明列联表
| 男 | 女 | 总计 | |
| 读营养说明 | 16 | 8 | 24 |
| 不读营养说明 | 4 | 12 | 16 |
| 总计 | 20 | 20 | 40 |
⑴根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
⑵从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注: ,其中
,其中 为样本容量.)
为样本容量.)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆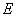 :
: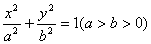 的右焦点
的右焦点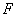 ,过原点和
,过原点和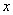 轴不重合的直线与椭圆
轴不重合的直线与椭圆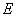 相交于
相交于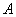 ,
,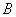 两点,且
两点,且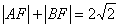 ,
,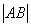 最小值为
最小值为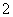 .
.
(Ⅰ)求椭圆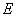 的方程;
的方程;
(Ⅱ)若圆: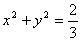 的切线
的切线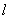 与椭圆
与椭圆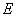 相交于
相交于 ,
,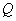 两点,当
两点,当 ,
,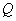 两点横坐标不相等时,问:
两点横坐标不相等时,问: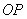 与
与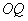 是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com