
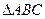 中,
中,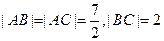 ,以
,以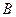 、
、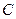 为焦点的椭圆恰好过
为焦点的椭圆恰好过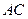 的中点
的中点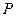 。
。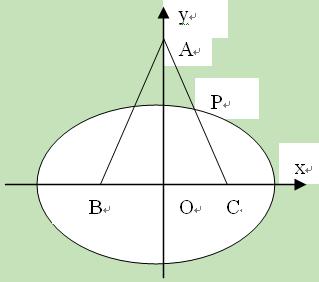
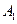 作直线
作直线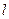 与圆
与圆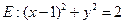 相交于
相交于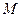 、
、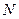 两点,试探究点
两点,试探究点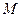 、
、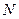 能将圆
能将圆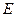 分割成弧长比值为
分割成弧长比值为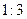 的两段弧吗?若能,求出直线
的两段弧吗?若能,求出直线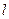 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.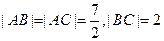 ∴
∴
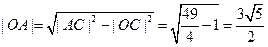 ………2分
………2分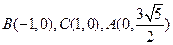 ∴
∴ ……4分
……4分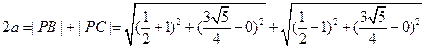

 ,…………………………………………………………………………6分
,…………………………………………………………………………6分 ,∴
,∴ ………………………………………………………7分
………………………………………………………7分 ……………………………………………8分
……………………………………………8分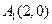 ,圆
,圆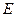 圆心为
圆心为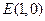 ,半径
,半径 。
。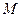 、
、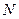 能将圆
能将圆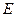 分割成弧长比值为
分割成弧长比值为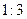 的两段弧,
的两段弧, ,圆心
,圆心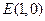 到直线
到直线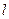 的距离
的距离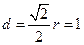 ………………10分
………………10分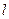 斜率不存在时,
斜率不存在时,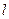 的方程为
的方程为 ,
,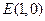 到直线
到直线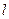 的距离
的距离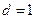 (符合)……………………………11分
(符合)……………………………11分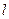 斜率存在时,设
斜率存在时,设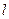 的方程为
的方程为 ,即
,即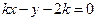 ,
,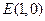 到直线
到直线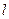 的距离
的距离 ,无解……………………………13分
,无解……………………………13分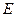 分割成弧长比值为
分割成弧长比值为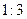 的两段弧,此时
的两段弧,此时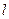 方程为
方程为 …14分。
…14分。

科目:高中数学 来源:不详 题型:解答题
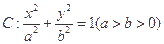 的离心率为
的离心率为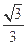 ,过右焦点F的直线
,过右焦点F的直线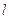 与
与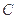 相交于
相交于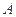 、
、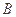 两点,当
两点,当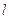 的斜率为1时,坐标原点
的斜率为1时,坐标原点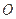 到
到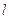 的距离为
的距离为
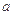 ,
,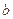 的值;
的值;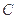 上是否存在点P,使得当
上是否存在点P,使得当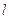 绕F转到某一位置时,有
绕F转到某一位置时,有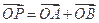 成立?
成立?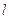 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
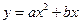 (a
(a 0)与双曲线
0)与双曲线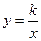 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).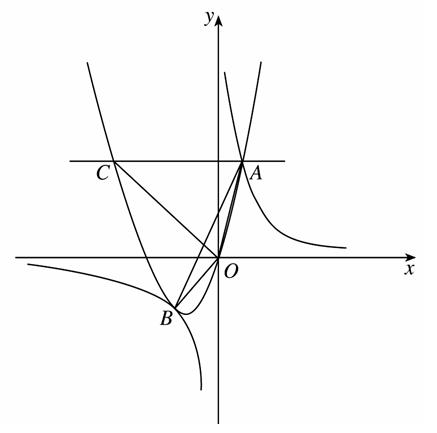
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
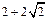 .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W.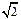 )且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;
)且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;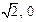 ),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量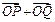 与
与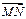 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com