Question

某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y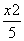＝－48x＋8 000，已知此生产线年产量最大为210吨．

(1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；

(2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？

Answer 1

解： (1)每吨平均成本为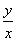(万元)．则（方法一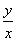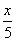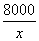）＝＋－48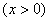，----2分

设，，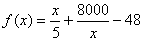

令=0，得x＝200（舍去负值），----4分

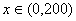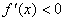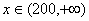时，，时，，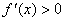

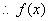在x＝200处取得极小值也是最小值--------5分

∴年产量为200吨时，每吨平均成本最低为32万元．------6分

（方法二）

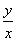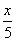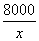＝＋－48≥2 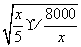－48＝32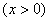，-------4分

当且仅当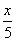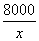＝，即x＝200时取等号．---------5分

∴年产量为200吨时，每吨平均成本最低为32万元．------6分

(2)设年获得总利润为R(x)万元，

则R(x)＝40x－y＝40x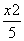－＋48x－8 000

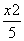＝－＋88x－8 000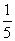＝－(x－220)²＋1 680(0≤x≤210)．------9分

∵R(x)在[0,210]上是增函数，∴x＝210时，R(x)有最大值为

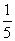－(210－220)²＋1 680＝1 660.--------11分

∴年产量为210吨时，可获得最大利润1 660万元．-----12分