
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() (
(![]() ,
, ![]() ).
).

(1)设![]() 中点为
中点为![]() ,
, ![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)延长三棱台![]() 的三条侧棱,设交点为
的三条侧棱,设交点为![]() ,
, ![]() 时
时![]() 为
为![]() 的中点,设
的中点,设![]() 中点为
中点为![]() ,连
,连![]() 梯形
梯形![]() 中,中位线
中,中位线![]() ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得![]() 平面
平面![]() ;同理可证
;同理可证![]() 平面
平面![]() ,然后再根据面面平行的判定定理可得,平面
,然后再根据面面平行的判定定理可得,平面![]() 平面
平面![]() ,进而可证命题成立;(2)设
,进而可证命题成立;(2)设![]() 中点为
中点为![]() ,连
,连![]() ,在
,在![]() 中作
中作![]() 且交
且交![]() 于点
于点![]() ,由面面垂直的性质定理,可得
,由面面垂直的性质定理,可得![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 为
为![]() 到平面
到平面![]() 的距离,
的距离, ![]()
且![]() 为直线
为直线![]() 与平面
与平面![]() 所成角;再根据面面垂直的性质定理,可得
所成角;再根据面面垂直的性质定理,可得![]() 可得
可得![]() ,
, ![]() 中
中![]() 为
为![]() 的中点
的中点![]()
![]() ,由此即可求出线面角的正弦值.
,由此即可求出线面角的正弦值.
试题解析:
(1)延长三棱台![]() 的三条侧棱,设交点为
的三条侧棱,设交点为![]()
![]() 时
时![]() 为
为![]() 的中点,
的中点,
设![]() 中点为
中点为![]() ,连
,连![]()
梯形![]() 中,中位线
中,中位线![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]() ;
;
![]() 中,中位线
中,中位线![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() 且
且![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以平面![]() 平面
平面![]()
所以![]() 平面
平面![]()
(2)设![]() 中点为
中点为![]() ,连
,连![]() ,在
,在![]() 中作
中作![]() 且交
且交![]() 于点
于点![]() ,
,

又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 为
为![]() 到平面
到平面![]() 的距离,
的距离, ![]()
且![]() 为直线
为直线![]() 与平面
与平面![]() 所成角
所成角
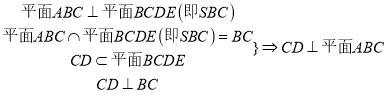
![]() 平面
平面![]() ,所以
,所以![]() ,
, ![]() 中
中![]()
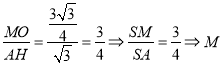 为
为![]() 的中点
的中点
![]()
![]()
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知Sn是等差数列{an}的前n项和,且S8>S9>S7 , 给出下列四个命题:
①d<0;
②S16<0;
③数列{Sn}中的最大项为S15;
④|a8|>|a9|.
其中正确命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,且
,且![]() ,设命题p:函数
,设命题p:函数![]() 在
在![]() 上单调递减;命题q:函数
上单调递减;命题q:函数![]() 在
在![]() 上为增函数,
上为增函数,
(1)若“p且q”为真,求实数c的取值范围
(2)若“p且q”为假,“p或q”为真,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
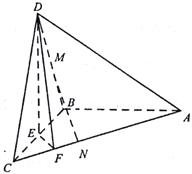
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 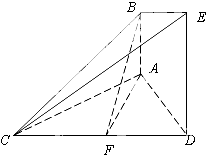
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com