
【题目】为了解社会对学校办学质量的满意程度,某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取![]() 人进行问卷调查,已知高一、高二、高三、的家长委员会分别有
人进行问卷调查,已知高一、高二、高三、的家长委员会分别有![]() 人,
人,![]() 人,
人,![]() 人.
人.
![]() 求从三个年级的家长委员会分别应抽到的家长人数;
求从三个年级的家长委员会分别应抽到的家长人数;
![]() 若从抽到的
若从抽到的![]() 人中随机抽取
人中随机抽取![]() 人进行调查结果的对比,求这
人进行调查结果的对比,求这![]() 人中至少有一人是高三学生家长的概率.
人中至少有一人是高三学生家长的概率.
【答案】(1) 3,1,2 (2)![]()
【解析】
试题(I)由题意知总体个数是54+18+36,要抽取的个数是6,做出每个个体被抽到的概率,分别用三个年级的数目乘以概率,得到每一个年级要抽取的人数.(II)本题为古典概型,先将各区所抽取的家长用字母表达,分别计算从抽取的6个家长中随机抽取2个的个数和至少有1个来自高三的个数,再求比值即可
试题解析:(1)家长委员会人员总数为54+18+36=108,
样本容量与总体中的个体数的比为![]() ,
,
故从三个年级的家长委员会中分别抽取的人数为3,1,2.
(2)得A1,A2,A3为从高一抽得的3个家长,B1为从高二抽得的1个家长,C1,C2为从高三抽得的2个家长.
则抽取的全部结果有:
(A1,A2),(A1,A3),(A1,B1),(A1,C1),(A1,C2),(A2,A3),(A2,B1),(A2,C1),(A2,C2),(A3,B1),(A3,C1),(A3,C2),(B1,C1),(B1,C2),(C1,C2),共15种.
令X=“至少有一人是高三学生家长”,结果有:
(A1,C1),(A1,C2),(A2,C1),(A2,C2),(A3,C1),(A3,C2),(B1,C1),(B1,C2),(C1,C2),共9种,所以这2人中至少有1人是高三学生家长的概率是P(X)=![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() ,
,![]() 是线段
是线段![]() 上一点.
上一点.
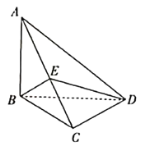
(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(2)是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,请指出点
?若存在,请指出点![]() 的位置,并加以证明;若不存在,请说明理由.
的位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在D上的函数f(x)满足:对任意x∈D,存在常数M>0,都有-M<f(x)<M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界。
(Ⅰ)判断函数f(x)=![]() -2x+2,x∈[0,2]是否是有界函数,请说明理由;
-2x+2,x∈[0,2]是否是有界函数,请说明理由;
(Ⅱ)若函数f(x)=1+![]() +
+![]() ,x∈[0,+∞)是以3为上界的有界函数,求实数a的取值范围。
,x∈[0,+∞)是以3为上界的有界函数,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读材料:空间直角坐标系O﹣xyz中,过点P(x0,y0,z0)且一个法向量为![]() =(a,b,c)的平面α的方程为a(x﹣x0)+b(y﹣y0)+c(z﹣z0)=0;过点P(x0,y0,z0)且一个方向向量为
=(a,b,c)的平面α的方程为a(x﹣x0)+b(y﹣y0)+c(z﹣z0)=0;过点P(x0,y0,z0)且一个方向向量为![]() =(u,v,w)(uvw≠0)的直线l的方程为
=(u,v,w)(uvw≠0)的直线l的方程为![]() ,阅读上面材料,并解决下面问题:已知平面α的方程为x+2y﹣2z﹣4=0,直线l是两平面3x﹣2y﹣7=0与2y﹣z+6=0的交线,则直线l与平面α所成角的大小为( )
,阅读上面材料,并解决下面问题:已知平面α的方程为x+2y﹣2z﹣4=0,直线l是两平面3x﹣2y﹣7=0与2y﹣z+6=0的交线,则直线l与平面α所成角的大小为( )
A. arcsin![]() B. arcsin
B. arcsin![]()
C. arcsin![]() D. arcsin
D. arcsin![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]()
(1)若4比![]() 接近0,求
接近0,求![]() 的取值范围;
的取值范围;
(2)对于任意的两个不等正数![]() ,求证:
,求证:![]() 比
比![]() 接近
接近![]() ;
;
(3)若对于任意的非零实数![]() ,实数
,实数![]() 比
比![]() 接近
接近![]() ,求
,求![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com