
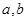 .
.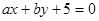 与圆
与圆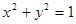 相切的概率;
相切的概率;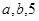 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.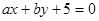 与圆
与圆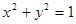 相切的概率为
相切的概率为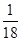 ;
;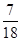 .
.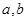 事件总数为36,直线
事件总数为36,直线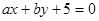 与圆
与圆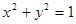 相切只有两种情况,所以相切的概率为
相切只有两种情况,所以相切的概率为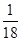 ;
;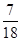 .
.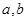 ,事件总数为6×6=36.
,事件总数为6×6=36. 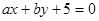 与圆
与圆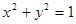 相切,所以有
相切,所以有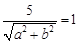 即:
即: ,由于
,由于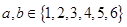
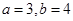 或
或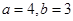 两种情况.
两种情况.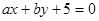 与圆
与圆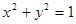 相切的概率是
相切的概率是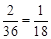
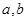 ,事件总数为6×6=36.
,事件总数为6×6=36.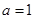 时,
时,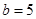 ,(1,5,5) 1种
,(1,5,5) 1种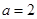 时,
时,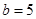 ,(2,5,5) 1种
,(2,5,5) 1种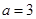 时,
时,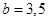 ,(3,3,5),(3,5,5) 2种
,(3,3,5),(3,5,5) 2种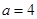 时,
时,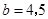 ,(4,4,5),(4,5,5) 2种
,(4,4,5),(4,5,5) 2种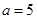 时,
时,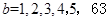 ,
,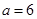 时,
时, ,(6,5,5),(6,6,5) 2种
,(6,5,5),(6,6,5) 2种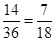 .
.

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 评估的平均得分 |  |  |  |
| 全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 | 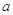 6 6 |
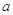 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下: |  |
 |  |
 ppm.
ppm. 条鱼中,随机抽出
条鱼中,随机抽出 条,求
条,求 条中恰有
条中恰有 条汞含量超标的概率;
条汞含量超标的概率; 条鱼,记
条鱼,记 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com