
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(1)求an,bn; (2)求数列{an·bn}的前n项和Tn.
(1)an=4n-1,bn=2n-1(n∈N*);(2)Tn=5+(4n-5)×2n.
解析试题分析:(1)本小题中已知Sn是数列{an}的前n项和,且Sn的表达式已知,当n≥2时,an=Sn-Sn-1,而当n=1时,a1=S1且检查是否符合前式,在an求出之后利用an=4log2bn+3求得bn;(2)可知an·bn的表达式是等差乘以等比形式,求这类数列的前n项和Tn,只需用错位相减法可完成求和,即若等比数列的公比为q,则由Tn -qTn进行错位相减,整理出Tn即可.
试题解析:(1)由Sn=2n2+n,可得:当n≥2时,an=Sn-Sn-1=(2n2+n)-[2(n-1)2+(n-1)]="4n-1," 当n=1时,a1=3符合上式,所以an=4n-1(n∈N*).由an=4log2bn+3,可得4n-1=4log2bn+3, 解得bn=2n-1(n∈N*).
(2)anbn=(4n-1)·2n-1, ∴Tn=3+7×21+11×22+15×23+…+(4n-1)×2n-1, ①
2Tn=3×21+7×22+11×23+15×24+…+(4n-1)×2n, ②
①-②可得:
-Tn=3+4[21+22+23+24+…+2n-1]-(4n-1)×2n=3+4×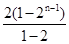 -(4n-1)×2n=-5+(5-4n)×2n,
-(4n-1)×2n=-5+(5-4n)×2n,
∴Tn=5+(4n-5)×2n.
考点: 与
与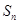 的关系:
的关系: ,错位相减法求和.
,错位相减法求和.


科目:高中数学 来源: 题型:解答题
给定数列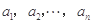 .对
.对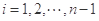 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后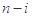 项
项 的最小值记为
的最小值记为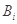 ,
,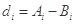 .
.
(1)设数列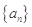 为3,4,7,1,写出
为3,4,7,1,写出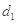 ,
,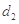 ,
,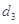 的值;
的值;
(2)设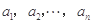 (
( )是公比大于1的等比数列,且
)是公比大于1的等比数列,且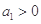 .证明:
.证明: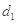 ,
,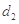 ,…,
,…,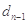 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列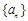 的前n项和为
的前n项和为 满足:
满足: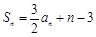 .
.
(1)求证:数列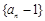 是等比数列;
是等比数列;
(2)令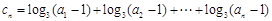 ,对任意
,对任意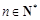 ,是否存在正整数m,使
,是否存在正整数m,使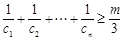 都成立?若存在,求出m的值;若不存在,请说明理由.
都成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
等比数列{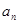 }的公比为q,其前n项和的积为Tn,并且满足下面条件
}的公比为q,其前n项和的积为Tn,并且满足下面条件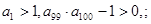
 给出下列结论:①0<q<1;②a99·a100—1<0;③T100的值是Tn中最大的;④使Tn>1成立的最大自然数n等于198.其中正确的结论是:
给出下列结论:①0<q<1;②a99·a100—1<0;③T100的值是Tn中最大的;④使Tn>1成立的最大自然数n等于198.其中正确的结论是:
(写出所有正确命题的序号)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com