
图是某市 月
月 日至
日至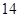 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(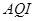 )小于
)小于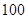 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于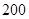 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择 月
月 日至
日至 月
月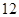 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留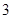 天.
天.
(1)求此人到达当日空气质量重度污染的概率;
(2)设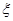 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求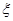 的分布列与数学期望.
的分布列与数学期望.
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
袋中装有若干个质地均匀大小一致的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(1)求摸球3次就停止的事件发生的概率;
(2)记摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及其期望.
的分布列及其期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市公租房的房源位于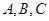 三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(1)恰有2人申请 片区房源的概率;
片区房源的概率;
(2)申请的房源所在片区的个数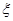 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为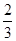 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为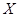 ,试求
,试求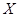 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中有 个白球和
个白球和 个红球(
个红球( ,且
,且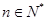 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若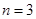 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为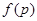 ,当
,当 为何值时,
为何值时,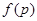 取最大值.
取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位从一所学校招收某类特殊人才.对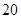 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
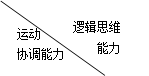 | 一般 | 良好 | 优秀 |
| 一般 |  |  |  |
| 良好 | 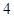 |  |  |
| 优秀 |  |  | 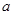 |
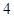 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这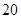 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为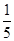 .
.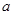 ,
, 的值;
的值; 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如下表
| 环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 1 | 2 | 4 |
| 环数 | 7 | 8 | 9 | 10 |
| 概率 | 0.2 | 0.3 | p | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表中有三个游戏规则,袋子中分别装有大小相同的球,从袋子中取球,分别计算甲获胜的概率,说明哪个游戏是公平的?
| 游戏1 | 游戏2 | 游戏3 |
| 1个红球和1个白球 | 2个红球和2个白球 | 3个红球和1个白球 |
| 取1个球 | 取1个球,再取1个球 | 取1个球,再取1个球 |
| 取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
| 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com