
甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如下表
| 环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 1 | 2 | 4 |
| 环数 | 7 | 8 | 9 | 10 |
| 概率 | 0.2 | 0.3 | p | 0.1 |
(1) 0.21 p=0.4
解析解:(1)由0.2+0.3+p+0.1=1,得p=0.4.
设甲,乙两人击中的环数分别为X1,X2,则
P(X1=8)=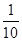 =0.1,
=0.1,
P(X1=9)=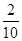 =0.2,
=0.2,
P(X1=10)=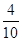 =0.4;
=0.4;
P(X2=8)=0.3,
P(X2=9)=0.4,
P(X2=10)=0.1,
所以甲,乙各打一枪共击中18环的概率为:
P=0.1×0.1+0.3×0.4+0.2×0.4=0.21.
(2)甲的期望E(X1)=5×0.1+6×0.1+7×0.1+8×0.1+9×0.2+10×0.4=8.4.
乙的期望E(X2)=7×0.2+8×0.3+9×0.4+10×0.1=8.4.
甲的方差D(X1)=(5-8.4)2×0.1+(6-8.4)2×0.1+(7-8.4)2×0.1+(8-8.4)2×0.1+(9-8.4)2×0.2+(10-8.4)2×0.4=3.04.
乙的方差为D(X2)=(7-8.4)2×0.2+(8-8.4)2×0.3+(9-8.4)2×0.4+(10-8.4)2×0.1=0.84.
由于D(X1)>D(X2),故乙比甲技术稳定.


科目:高中数学 来源: 题型:解答题
在一次面试中,每位考生从4道题a、b、c、d中任抽两题做,假设每位考生抽到各题的可能性相等,且考生相互之间没有影响.
(1)若甲考生抽到a、b题,求乙考生与甲考生恰好有一题相同的概率;
(2)设某两位考生抽到的题中恰好有X道相同,求随机变量X的概率分布.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
图是某市 月
月 日至
日至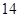 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(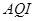 )小于
)小于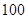 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于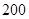 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择 月
月 日至
日至 月
月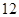 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留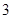 天.
天.
(1)求此人到达当日空气质量重度污染的概率;
(2)设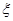 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求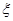 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出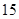 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
 | 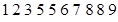 |
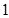 | 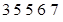 |
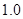 ppm.
ppm.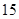 条鱼中,随机抽出
条鱼中,随机抽出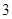 条,求
条,求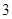 条中恰有
条中恰有 条汞含量超标的概率;
条汞含量超标的概率;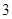 条鱼,记
条鱼,记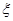 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此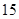 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求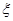 的分布列及数学期望
的分布列及数学期望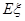 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医院一天派出医生下乡医疗,派出医生人数及其概率如下:
| 医生人数 | 0 | 1 | 2 | 3 | 4 | 5人及以上 |
| 概率 | 0.1 | 0.16 | x | y | 0.2 | z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求: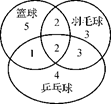
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com