
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某射击小组有甲、乙两名射手,甲的命中率为P1= ,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
(1)若P2= ,求该小组在一次检测中荣获“先进和谐组”的概率;
,求该小组在一次检测中荣获“先进和谐组”的概率;
(2)计划在2013年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数为ξ,如果E(ξ)≥5,求P2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为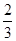 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为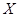 ,试求
,试求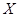 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位从一所学校招收某类特殊人才.对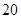 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
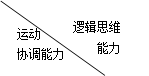 | 一般 | 良好 | 优秀 |
| 一般 |  |  |  |
| 良好 | 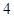 |  |  |
| 优秀 |  |  | 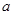 |
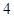 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这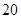 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为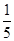 .
.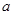 ,
, 的值;
的值; 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某大厦的一部电梯从底层出发后只能在第18,19,20层可以停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为 ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如下表
| 环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 1 | 2 | 4 |
| 环数 | 7 | 8 | 9 | 10 |
| 概率 | 0.2 | 0.3 | p | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中有4个红球,3个黑球,从袋中随机地抽取4个球,设取到1个红球得2分,取到1个黑球得1分.
(1)求得分X的分布列;(2)求得分大于6的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位招聘职工,经过几轮筛选,一轮从2000名报名者中筛选300名进入二轮笔试,接着按笔试成绩择优取100名进入第三轮面试,最后从面试对象中综合考察聘用50名.
(1)求参加笔试的竞聘者能被聘用的概率;
(2)用分层抽样的方式从最终聘用者中抽取10名进行进行调查问卷,其中有3名女职工,求被聘用的女职工的人数;
(3)单位从聘用的三男和二女中,选派两人参加某项培训,至少选派一名女同志参加的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com