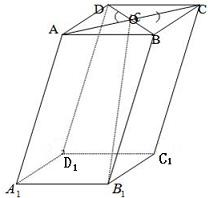
分析:根据平行六面体ABCD-A1B1C1D1中,三棱锥B1-ABC为正四面体,可得该几何体各棱及每个面的较短的对角线均相等,进而由正四面体的几何特征还可得到四棱锥B1-ACC1A1和四棱锥D-ACC1A1均为正四棱锥,连接B1D交平面ACC1A1于O,延长A1A至E,使A1A=AE,连接AD1,DE,可得∠OED即为直线AD1与平面ACC1A1所成角,解△OED可得答案.
解答:
解:∵平行六面体ABCD-A
1B
1C
1D
1中,三棱锥B
1-ABC为正四面体,
故B
1C=B
1A=B
1A
1=B
1C
1,即四棱锥B
1-ACC
1A
1为正四棱锥,
同理,四棱锥D-ACC
1A
1也为正四棱锥,
连接B
1D交平面ACC
1A
1于O,则O即为D在平面ACC
1A
1上的射影
延长A
1A至E,使A
1A=AE,连接AD
1,DE,
则DE∥AD
1,
则∠OED即为直线AD
1与平面ACC
1A
1所成角
设平行六面体ABCD-A
1B
1C
1D
1各棱长均为a
在Rt△OED中,OD为棱长均为a的正四棱锥的高,故OD=
=
a,
OE=
=
a,
DE=
=
a∴sin∠OED=
=
=
故答案为:
点评:本题考查的知识点是直线与平面所成的角,其中根据已知条件,结合正四面体的几何特征,分析出∠OED即为直线AD1与平面ACC1A1所成角,将线面夹角问题转化为解三角形问题是解答的关键.

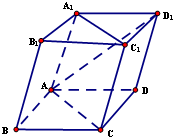 在平行六面体ABCD-A1B1C1D1中,三棱锥B1-ABC为正四面体,则直线AD1与平面ACC1A1所成角的正弦值为
在平行六面体ABCD-A1B1C1D1中,三棱锥B1-ABC为正四面体,则直线AD1与平面ACC1A1所成角的正弦值为 解:∵平行六面体ABCD-A1B1C1D1中,三棱锥B1-ABC为正四面体,
解:∵平行六面体ABCD-A1B1C1D1中,三棱锥B1-ABC为正四面体,

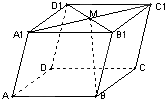 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若