
A、
| ||||||
B、1-
| ||||||
C、1-
| ||||||
| D、1 |
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
9
| ||
| 16 |
A、
| ||
B、
| ||
| C、16π | ||
| D、9π |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、10米/秒 | B、8米/秒 |
| C、12米/秒 | D、6米/秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| 7π |
| 12 |
| π |
| 12 |
查看答案和解析>>
科目:高中数学 来源:2015届宁夏银川市高三9月月考文科数学试卷(解析版) 题型:填空题
对于函数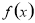 ,若存在区间
,若存在区间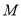 =[
=[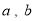 ](
](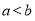 ),使得
),使得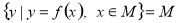 ,则称区间
,则称区间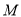 为函数
为函数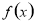 的一个“稳定区间”.给出下列四个函数:
的一个“稳定区间”.给出下列四个函数:
①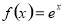 ②
②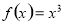 ③
③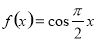 ④
④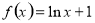
其中存在“稳定区间”的函数有_____________(填正确序号).
查看答案和解析>>
科目:高中数学 来源:2015届宁夏高三上学期第二次月考试卷文科数学试卷(解析版) 题型:解答题
已知曲线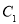 :
: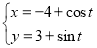 (
(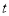 为参数),
为参数),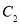 :
: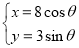 (
(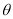 为参数).
为参数).
(1)化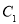 ,
,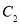 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若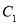 上的点
上的点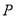 对应的参数为
对应的参数为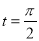 ,
,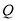 为
为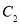 上的动点,求
上的动点,求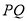 中点
中点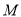 到直线
到直线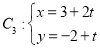 (
(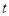 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com