
【题目】已知以点![]() 为圆心的圆过原点
为圆心的圆过原点![]() .
.
(1)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若
,若![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)在(1)的条件下,设![]() ,且
,且![]() 分别是直线
分别是直线![]() 和圆
和圆![]() 上的动点,求
上的动点,求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
试题分析:(1)![]() ,所以原点
,所以原点![]() 在
在![]() 的中垂线上.利用两条直线斜率乘积等于
的中垂线上.利用两条直线斜率乘积等于![]() ,解得
,解得![]() 或
或![]() ,经验证
,经验证![]() 不符合题意,所以
不符合题意,所以![]() ,圆的方程为
,圆的方程为![]() ;(2)在三角形
;(2)在三角形![]() 中,两边之差小于第三边,故
中,两边之差小于第三边,故![]() ,又
,又![]() 三点共线时
三点共线时![]() 最大,所以
最大,所以![]() 的最大值为
的最大值为![]() .线
.线![]() 的方程为
的方程为![]() 与
与![]() 联立求得交点为
联立求得交点为![]() .
.
试题解析:
(1)∵![]() ,所以,则原点
,所以,则原点![]() 在
在![]() 的中垂线上.
的中垂线上.
设![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
∴![]() 三点共线.
三点共线.
∵直线![]() 的方程是
的方程是![]() ,∴直线
,∴直线![]() 的斜率
的斜率 ,解得
,解得![]() 或
或![]() ,
,
∴圆心为![]() 或
或![]() ,
,
∴圆![]() 的方程为
的方程为![]() 或
或![]() .
.
由于当圆方程为![]() 时,圆心到直线
时,圆心到直线![]() 的距离
的距离![]() ,
,
此时不满足直线与圆相交,故舍去.
∴圆![]() 的方程为
的方程为![]() .
.
(2)在三角形![]() 中,两边之差小于第三边,故
中,两边之差小于第三边,故![]() ,
,
又![]() 三点共线时
三点共线时![]() 最大,
最大,
所以![]() 的最大值为
的最大值为![]() .
.
∵![]() ,
,![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,
,
∴直线![]() 与直线
与直线![]() 的交点
的交点![]() 的坐标为
的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
,![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中开展了丰富多彩的社团文化活动,甲,乙,丙三位同学在被问到是否参加过街舞社,动漫社,器乐社这三个社团时,
甲说:我参加过的社团比乙多,但没有参加过动漫社;
乙说:我没有参加过器乐社;
丙说:我们三个人都参加过同一个社团,由此判断乙参加过的社团为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点.如果x1+x2=6, 那么|AB|=( )
A. 6 B. 8
C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
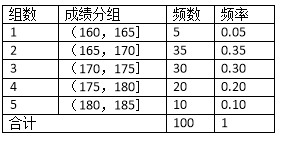
(1)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com