
【题目】下列说法正确的个数有( )
①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差;反之,则越好;
越大时,模型的拟合效果越差;反之,则越好;
②命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
③若回归直线的斜率估计值是![]() ,样本点的中心为
,样本点的中心为![]() ,则回归直线方程是
,则回归直线方程是![]() ;
;
④综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”。
A. 1个 B. 2个 C. 3个 D. 4个
科目:高中数学 来源: 题型:
【题目】《张邱建算经》是中国古代数学史上的杰作,该书中有首古民谣记载了一数列问题:“南山一棵竹,竹尾风割断,剩下三十节,一节一个圈,头节高五寸①,头圈一尺三②,逐节多三分③,逐圈少分三④,一蚁往上爬,遇圈则绕圈。爬到竹子顶,行程是多远?”(注释:①第节的高度为0.5尺;②第一圈的周长为1.3尺;③每节比其下面的一节多0.03尺;④每圈周长比其下面的一圈少0.013尺),问:此民谣提出的问题的答案是( )
A. 61.395尺B. 61.905尺C. 72.705尺D. 73.995尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() 的左右焦点分别是F1 , F2 , 离心率为
的左右焦点分别是F1 , F2 , 离心率为 ![]() ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连接PF1 , PF2 , 设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1 , PF2的斜率分别为k1 , k2 , 若k≠0,试证明 ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组样本点![]() ,其中
,其中![]() .根据最小二乘法求得的回归方程是
.根据最小二乘法求得的回归方程是![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 若所有样本点都在![]() 上,则变量间的相关系数为1
上,则变量间的相关系数为1
B. 至少有一个样本点落在回归直线![]() 上
上
C. 对所有的预报变量![]() ,
,![]() 的值一定与
的值一定与![]() 有误差
有误差
D. 若![]() 斜率
斜率![]() ,则变量
,则变量![]() 与
与![]() 正相关
正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1+x)e﹣2x , g(x)=ax+ ![]() +1+2xcosx,当x∈[0,1]时,
+1+2xcosx,当x∈[0,1]时,
(1)求证: ![]() ;
;
(2)若f(x)≥g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1 , 直线C2的极坐标方程分别为ρ=4sinθ,ρcos( ![]() )=2
)=2 ![]() .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为 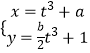 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)![]() 是{an}的前n项和,求
是{an}的前n项和,求![]() 的最大值。
的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com