练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆长轴上有一点到两个焦点之间的距离分别为：3＋2，3－2

     （1）求椭圆的方程；

     （2）如果直线x=t(teR）与椭圆相交于A,B，若C（－3,0），D(3,0），证明直线CA与直线

    BD的交点K必在一条确定的双曲线上；

      （3）过点Q(1,0 )作直线l(与x轴不垂直）与椭圆交于M,N两点，与y轴交于点R，、若

    ，求证：为定值．

     

    【答案】

    （1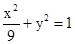）．（2）直线CA与直线BD的交点K必在双曲线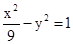上

    （3）λ+μ=-．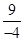

    【解析】本试题主要是考查了圆锥曲线方程的求解，以及直线与圆锥曲线的位置关系的综合运用。

    （1）因为椭圆长轴上有一点到两个焦点之间的距离分别为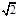：3＋2，3－2可知2a=6,a=3,然后结合a,b,c关系的得到椭圆的方程；

    （2）因为 直线x=t(teR）与椭圆相交于A,B，若C（－3,0），D(3,0），要证明直线CA与直线BD的交点K必在一条确定的双曲线上；关键是表示出两条直线方程，然后得到证明。

    （3）过点Q(1,0 )作直线l(与x轴不垂直）与椭圆交于M,N两点，与y轴交于点R，联立方程组和韦达定理以及向量的关系式得到参数的关系式

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

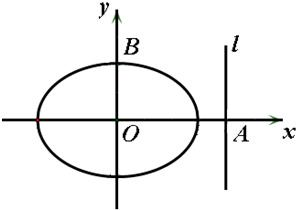    精英家教网已知椭圆E：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的离心率为
    		2
    2
    ，且过点P(2，
    		2
    )    ，设椭圆的右准线l与x轴的交点为A，椭圆的上顶点为B，直线AB被以原点为圆心的圆O所截得的弦长为
    4
    		5
    5
    ．
    （1）求椭圆E的方程及圆O的方程；
    （2）若M是准线l上纵坐标为t的点，求证：存在一个异于M的点Q，对于圆O上任意一点N，有
    MN
    NQ
    为定值；且当M在直线l上运动时，点Q在一个定圆上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

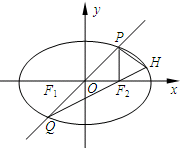    已知椭圆
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的左、右焦点分别为F1，F2．
    （Ⅰ）若椭圆的焦距为2
    		3
    ，且两条准线间的距离为
    8
    		3
    3
    ，求椭圆的方程；
    （Ⅱ）在（I）的条件下，椭圆上有一点M，满足MF1⊥MF2，求△MF1F2的面积；
    （Ⅲ）过焦点F2作椭圆长轴的垂线与椭圆交于第一象限点P，连接PO并延长交椭圆于点Q，连接QF2并延长交椭圆于点H，若PH⊥PQ，求椭圆的离心率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•广东模拟）已知椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的上顶点为A（0，1），过C1的焦点且垂直长轴的弦长轴的弦长为1．
    （1）求椭圆C1的方程；
    （2）设圆O：x2+y2=
    4
    5
    ，过该圆上任意一点作圆的切线l，试证明l和椭圆C1恒有两个交点A，B，且有
    OA
    •
    OB
    =0    ；
    （3）在（2）的条件下求弦AB长度的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

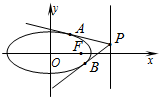    精英家教网已知椭圆的中心在坐标原点，焦点在x轴上，并且焦距为2，短轴与长轴的比是
    		3
    2
    ．
    （1）求椭圆的方程；
    （2）已知椭圆中有如下定理：过椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    上任意一点M（x0，y0）的切线唯一，且方程为
    x0x
    a2
    +
    y0y
    b2
    =1    ，利用此定理求过椭圆的点(1，
    3
    2
    )    的切线的方程；
    （3）如图，过椭圆的右准线上一点P，向椭圆引两条切线PA，PB，切点为A，B，求证：A，F，B三点共线．

    查看答案和解析>>

    同步练习册答案