
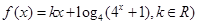 是偶函数.
是偶函数.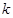 的值;
的值;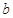 ,函数
,函数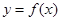 的图像与直线
的图像与直线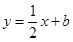 最多只有一个交点;
最多只有一个交点;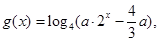 若函数
若函数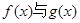 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数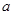 的取值范围.
的取值范围.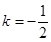 ;(2)证明见解析;(3)
;(2)证明见解析;(3)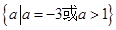 .
.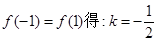 ,并进行检验;(2)原问题等价于证明方程组
,并进行检验;(2)原问题等价于证明方程组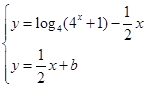 最多只有一组解,即证方程
最多只有一组解,即证方程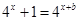 最多只有一个实根,利用反证法证明该方程不可能有两个实根,所以原命题得证;(3)问题转化为方程:
最多只有一个实根,利用反证法证明该方程不可能有两个实根,所以原命题得证;(3)问题转化为方程: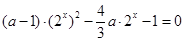 只有唯一解,令
只有唯一解,令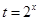 ,则可化为关于
,则可化为关于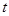 的方程:
的方程: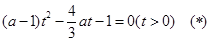 只有唯一正根,注意讨论二次项系数为0和不为0两种情形,当二次项系数不为0时,利用二次函数根的判定方法,最终可以得到所求实数
只有唯一正根,注意讨论二次项系数为0和不为0两种情形,当二次项系数不为0时,利用二次函数根的判定方法,最终可以得到所求实数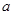 的取值范围.
的取值范围. 经检验的
经检验的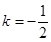 满足题意; 2分
满足题意; 2分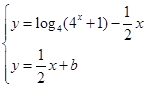 最多只有一组解,
最多只有一组解,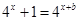 最多只有一个实根. 4分
最多只有一个实根. 4分 则有:
则有: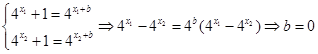 .
.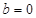 时,
时,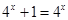 不成立.
不成立.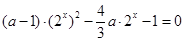 只有唯一解. 9分
只有唯一解. 9分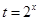 ,则可化为关于
,则可化为关于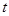 的方程:
的方程: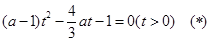 只有唯一正根. 10分
只有唯一正根. 10分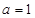 ,则上述方程变为
,则上述方程变为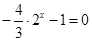 ,无解.故
,无解.故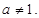 11分
11分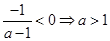 .此时方程(*)有唯一正根,满足条件; 12分
.此时方程(*)有唯一正根,满足条件; 12分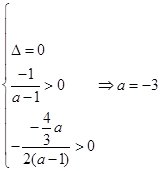 . 13分
. 13分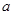 的取值范围是:
的取值范围是: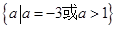 . 14分
. 14分

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:不详 题型:解答题
 度时,按每度
度时,按每度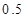 元计费,每月用电超过
元计费,每月用电超过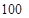 度时,超过部分按每度
度时,超过部分按每度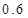 元计费,每月用电超过
元计费,每月用电超过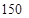 度时,超过部分按每度
度时,超过部分按每度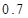 元计费
元计费 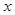 度,应交电费
度,应交电费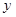 元,写出
元,写出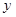 关于
关于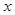 的函数;
的函数;| 月份 | 1 | 2 | 3 | 合计 |
| 缴费金额 | 87元 | 62元 | 45元8角 | 194元8角 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 若存在
若存在 ,使得
,使得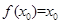 成立,则称
成立,则称 为
为 的不动点.
的不动点.
 时,求函数
时,求函数 的不动点;
的不动点;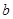 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围; 图象上
图象上 、
、 两点的横坐标是函数
两点的横坐标是函数 的不动点,且
的不动点,且 、
、 两点关于直线
两点关于直线 对称,求
对称,求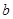 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
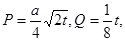 其中
其中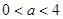 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.y=[ ] ] | B.y=[ ] ] | C.y=[ ] ] | D.y=[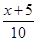 ] ] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com