
| 1 |
| 2x |
| π |
| 2 |
| 1 |
| 2-x |
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
| 2 |
| π |
| 4 |
| π |
| 2 |
|
| 2 |
| 2 |


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
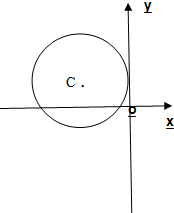 如图,已知位于y轴左侧的圆C与y轴相切于点(0,1),且被x轴分成的两段弧长之比为2:1,过点H(0,t)的直线l与圆C相交于M,N两点,且以MN为直径的圆恰好经过坐标原点O.
如图,已知位于y轴左侧的圆C与y轴相切于点(0,1),且被x轴分成的两段弧长之比为2:1,过点H(0,t)的直线l与圆C相交于M,N两点,且以MN为直径的圆恰好经过坐标原点O.查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是平行四边形,∠BAD=60°,AD=2,AC=2
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是平行四边形,∠BAD=60°,AD=2,AC=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
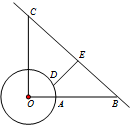 为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为
为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com