解:(I)设动点M的坐标为(x,y)
由题意得

=(x-1,y),

=(x+1,y)
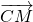
=(x,y-1),

=(x,y+1),

=(x,y)
∴

•

=x
2-1+y
2,
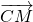
•

-
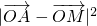
=x
2+y
2-1=y
2-1
化简得动点M的轨迹方程为x
2+(1-m)y
2=1-m
当m=1时,x
2=0,即x=0,动点M的轨迹是一条直线;
当m≠1时,方程可以化为:
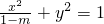
此时,当m=0时,动点M的轨迹是一个圆;
当m<0,或0<m<1时,动点M的轨迹是一个椭圆
当m>1时,动点M的轨迹是一条双曲线
(II)当m≠1且m≠0时,由
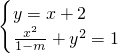
得x
2+(1-m)(x
2+4x+4)=1-m∴(2-m)x
2+4(1-m)x+3(1-m)=0
∵l与该圆锥曲线交于不同的两个点∴
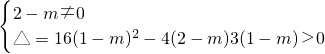
即
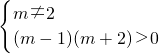
∴m>1且m≠2或m<-2
(1)m>1且m≠2时,圆锥曲线表示双曲线
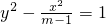
其中,a
2=1,b
2=m-1,c
2=m∴
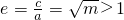
且

(2)当m<-2时,该圆锥曲线表示椭圆:
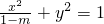
其中a
2=1-m,b
2=1,c
2=-m∵
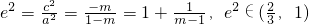
∴

综上:该圆锥曲线的离心率e的取值范围是
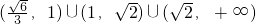
.
分析:(I)设M(x,y),利用题目中向量的坐标运算,求得向量的坐标后代入题中向量条件,化简即得轨迹方程,为了说明它是什么类型,必须对参数m进行讨论;
(II)将直线的方程代入圆锥曲线的方程,消去y得到关于x的一元二次方程,再结合根的判别式求得m的范围,再分类讨论:(1)m>1且m≠2时,(2)当m<-2时,分别求出该圆锥曲线的离心率e的取值范围即可.
点评:本题主要考查了轨迹方程的问题、直线与圆锥曲线的综合问题、向量的坐标运算,考查分类讨论思想以及等价转化能力.

 在直角坐标系XOY中,已知点A(1,0),B(-1,0),C(0,1),D(0,-1),动点M满足
在直角坐标系XOY中,已知点A(1,0),B(-1,0),C(0,1),D(0,-1),动点M满足 •
• =m(
=m(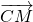 •
• -|
-| -
- |),其中m是参数(m∈R)
|),其中m是参数(m∈R) =(x-1,y),
=(x-1,y), =(x+1,y)
=(x+1,y)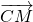 =(x,y-1),
=(x,y-1), =(x,y+1),
=(x,y+1), =(x,y)
=(x,y) •
• =x2-1+y2,
=x2-1+y2,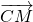 •
• -
-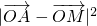 =x2+y2-1=y2-1
=x2+y2-1=y2-1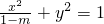
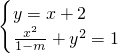 得x2+(1-m)(x2+4x+4)=1-m∴(2-m)x2+4(1-m)x+3(1-m)=0
得x2+(1-m)(x2+4x+4)=1-m∴(2-m)x2+4(1-m)x+3(1-m)=0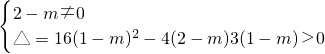
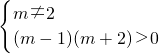 ∴m>1且m≠2或m<-2
∴m>1且m≠2或m<-2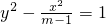
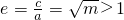 且
且
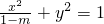
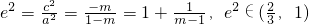 ∴
∴
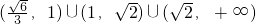 .
.

 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2