
| A.1 | B.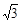 | C.2 | D.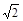 |
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源:不详 题型:单选题
| A.底面是正方形,有两个侧面垂直于底面 |
| B.底面是正方形,有两个侧面是矩形 |
| C.底面是菱形,且有一个顶点处的三条棱两两垂直 |
| D.每个底面是全等的矩形 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 表示两个不同的平面,l表示既不在a内也不在
表示两个不同的平面,l表示既不在a内也不在 内的直线,存在以下
内的直线,存在以下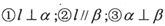 .若以其中两个为条件,另一个为结论,构成命题,
.若以其中两个为条件,另一个为结论,构成命题,| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com